Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1. Đề thiếu
2. BĐT cần chứng minh tương đương:
\(a^4+b^4+c^4\ge abc\left(a+b+c\right)\)
Ta có:
\(a^4+b^4+c^4\ge\dfrac{1}{3}\left(a^2+b^2+c^2\right)^2\ge\dfrac{1}{3}\left(ab+bc+ca\right)^2\ge\dfrac{1}{3}.3abc\left(a+b+c\right)\) (đpcm)
3.
Ta có:
\(\left(a^6+b^6+1\right)\left(1+1+1\right)\ge\left(a^3+b^3+1\right)^2\)
\(\Rightarrow VT\ge\dfrac{1}{\sqrt{3}}\left(a^3+b^3+1+b^3+c^3+1+c^3+a^3+1\right)\)
\(VT\ge\sqrt{3}+\dfrac{2}{\sqrt{3}}\left(a^3+b^3+c^3\right)\)
Lại có:
\(a^3+b^3+1\ge3ab\) ; \(b^3+c^3+1\ge3bc\) ; \(c^3+a^3+1\ge3ca\)
\(\Rightarrow2\left(a^3+b^3+c^3\right)+3\ge3\left(ab+bc+ca\right)=9\)
\(\Rightarrow a^3+b^3+c^3\ge3\)
\(\Rightarrow VT\ge\sqrt{3}+\dfrac{6}{\sqrt{3}}=3\sqrt{3}\)
4.
Ta có:
\(a^3+1+1\ge3a\) ; \(b^3+1+1\ge3b\) ; \(c^3+1+1\ge3c\)
\(\Rightarrow a^3+b^3+c^3+6\ge3\left(a+b+c\right)=9\)
\(\Rightarrow a^3+b^3+c^3\ge3\)
5.
Ta có:
\(\dfrac{a}{b}+\dfrac{b}{c}\ge2\sqrt{\dfrac{a}{c}}\) ; \(\dfrac{a}{b}+\dfrac{c}{a}\ge2\sqrt{\dfrac{c}{b}}\) ; \(\dfrac{b}{c}+\dfrac{c}{a}\ge2\sqrt{\dfrac{b}{a}}\)
\(\Rightarrow\sqrt{\dfrac{b}{a}}+\sqrt{\dfrac{c}{b}}+\sqrt{\dfrac{a}{c}}\le\dfrac{a}{b}+\dfrac{b}{c}+\dfrac{c}{a}=1\)

a)\(a^2+ab+b^2=a^2+\dfrac{2ab}{2}+\left(\dfrac{b}{2}\right)^2+\dfrac{3b^2}{4}\)
\(=\left(a+\dfrac{b}{2}\right)^2+\dfrac{3b^2}{4}\ge0\forall a,b\)
b)\(a^4+b^4\ge a^3b+ab^3\)
\(\Leftrightarrow a^3\left(a-b\right)-b^3\left(a-b\right)\ge0\)
\(\Leftrightarrow\left(a^3-b^3\right)\left(a-b\right)\ge0\)
\(\Leftrightarrow\left(a-b\right)^2\left(a^2+ab+b^2\right)\ge0\forall a,b\)

Bằng phản chứng giả sử a và b đều âm
\(\Rightarrow a< 0,b< 0\Rightarrow a+b< 0\)
Mà theo đề: \(a+b>0\)---> Mâu thuẫn giả thiết, vậy có ít nhất 1 trong a,b phải dương

Lời giải:
\(\text{BĐT}\Leftrightarrow \left ( \frac{a^2}{b}-2a+b \right )+\left ( \frac{b^2}{c}-2b+c \right )+\left ( \frac{c^2}{a}-2c+a \right )\geq \frac{6(a^2+b^2+c^2)}{a+b+c}-2(a+b+c)\)
\(\Leftrightarrow \frac{(a-b)^2}{b}+\frac{(b-c)^2}{c}+\frac{(c-a)^2}{a}\geq \frac{2[(a-b)^2+(b-c)^2+(c-a)^2)]}{a+b+c}(1)\)
Do BĐT có tính hoán vị giữa các biến nên giả sử $b$ nằm giữa $a$ và $c$
Áp dụng BĐT Cauchy-Schwarz:
\(\Leftrightarrow \frac{(a-b)^2}{b}+\frac{(b-c)^2}{c}+\frac{(c-a)^2}{a}\geq \frac{[(a-b)+(b-c)+(a-c)]^2}{a+b+c}=\frac{4(a-c)^2}{a+b+c}(2)\)
Ta chỉ cần CM \(\frac{4(a-c)^2}{a+b+c}\geq \frac{2[(a-b)^2+(b-c)^2+(c-a)^2]}{a+b+c}(3)\Leftrightarrow (a-c)^2\geq (a-b)^2+(b-c)^2\)
\(\Leftrightarrow (b-a)(b-c)\leq 0\). Điều này luôn đúng với $b$ nằm giữa $a$ và $c$
Từ \((1);(2);(3)\Rightarrow \text{đpcm}\). Dấu $=$ xảy ra khi $a=b=c$

Ta có:
\(\left(a+b+c\right)^3=a^3+b^3+c^3+3\left(a+b\right)\left(b+c\right)\left(c+a\right)\)
Dễ dàng chứng minh được:
\(\left(a+b\right)\left(b+c\right)\left(c+a\right)\ge8abc\)
\(\Rightarrow\left(a+b+c\right)^3\ge a^3+b^3+c^3+24abc\)
Khi đó ta được bất đẳng thức:
\(\frac{\left(a+b+c\right)^3}{abc}+\frac{ab+bc+ca}{a^2+b^2+c^2}\ge\frac{a^3+b^3+c^3+24abc}{abc}+\frac{ab+bc+ca}{a^2+b^2+c^2}\)
Vậy ta cần chứng minh:
\(\frac{a^3+b^3+c^3+24abc}{abc}+\frac{ab+bc+ca}{a^2+b^2+c^2}\ge28\)
\(\Leftrightarrow\frac{a^2}{bc}+\frac{b^2}{ca}+\frac{c^2}{ab}+\frac{ab+bc+ca}{a^2+b^2+c^2}\ge4\)
Theo bất đẳng thức Bunhiacopxki dạng phân thức ta được:
\(\frac{a^2}{bc}+\frac{b^2}{ca}+\frac{c^2}{ab}\ge\frac{\left(a+b+c\right)^2}{ab+bc+ca}=\frac{a^2+b^2+c^2}{ab+bc+ca}+2\)
Để hoàn thành chứng minh ta cần chỉ ra được:
\(\frac{a^2+b^2+c^2}{ab+bc+ca}+2+\frac{ab+bc+ca}{a^2+b^2+c^2}\ge4\)
\(\Leftrightarrow\frac{a^2+b^2+c^2}{ab+bc+ca}+\frac{ab+bc+ca}{a^2+b^2+c^2}\ge2\)
Theo bất đẳng thức Cauchy thì bất đẳng thức cuối cùng hiển nhiên đúng.
Như vậy bất đẳng thức được chứng minh. Dấu đẳng thức xẩy ra tại \(a=b=c\)

Với mọi \(0< a< \dfrac{1}{2}\) ta có:
\(\left(\sqrt{2a}-1\right)^2\ge0\Rightarrow2a+1\ge2\sqrt{2a}\)
\(\Rightarrow1\ge2\sqrt{a}\left(\sqrt{2}-\sqrt{a}\right)\)
\(\Rightarrow\dfrac{1}{\sqrt{2}-\sqrt{a}}\ge2\sqrt{a}\)
Do đó:
\(\dfrac{2+\sqrt{2a}}{2-a}=\dfrac{2-a+a+\sqrt{2a}}{2-a}=1+\dfrac{\sqrt{a}\left(\sqrt{a}+\sqrt{2}\right)}{\left(\sqrt{2}-\sqrt{a}\right)\left(\sqrt{2}+\sqrt{a}\right)}=1+\dfrac{\sqrt{a}}{\sqrt{2}-\sqrt{a}}\ge1+\sqrt{a}.2\sqrt{a}=2a+1\)
Tương tự:
\(\dfrac{2+\sqrt{2b}}{2-b}\ge2b+1\)
Cộng vế:
\(\dfrac{2+\sqrt{2a}}{2-a}+\dfrac{2+\sqrt{2b}}{2-b}\ge2a+1+2b+1=4\) (đpcm)
Dấu "=" xảy ra khi \(a=b=\dfrac{1}{2}\)

Ta có:
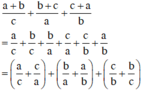
Áp dụng bất đẳng thức Cô-si cho hai số dương
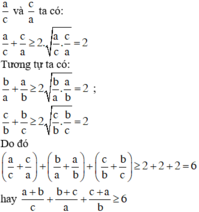
Dấu "=" xảy ra khi và chỉ khi a = b = c

\(3=a+b+ab\le a+b+\frac{\left(a+b\right)^2}{4}\Rightarrow\left(a+b\right)^2+4\left(a+b\right)-12\ge0\)
\(\Leftrightarrow\left(a+b-2\right)\left(a+b+6\right)\ge0\Rightarrow a+b\ge2\)
Đặt vế trái của BĐT là P
\(P=\frac{4a\left(a+1\right)+4b\left(b+1\right)}{\left(a+1\right)\left(b+1\right)}+2ab-\sqrt{7-3\left(3-a-b\right)}\)
\(P=\frac{4\left(a^2+b^2+a+b\right)}{ab+a+b+1}+2ab-\sqrt{3\left(a+b\right)-2}\)
\(P=a^2+b^2+a+b+2ab-\sqrt{3\left(a+b\right)-2}\)
\(P=\left(a+b\right)^2+a+b-\sqrt{3\left(a+b\right)-2}\)
Đặt \(\sqrt{3\left(a+b\right)-2}=x\Rightarrow\left\{{}\begin{matrix}x\ge2\\a+b=\frac{x^2+2}{3}\end{matrix}\right.\)
\(\Rightarrow P=\left(\frac{x^2+2}{3}\right)^2+\frac{x^2+2}{3}-x=\frac{x^4+7x^2-9x+10}{9}\)
\(P=\frac{x^4+7x^2-9x-26+36}{9}=\frac{\left(x-2\right)\left(x^3+2x^2+11x+13\right)}{9}+4\ge4\) ; \(\forall x\ge2\) (đpcm)
Dấu "=" xảy ra khi \(x=2\) hay \(a=b=1\)
Với 2 số dương a,b ta có:
(√a - √b )2 ≥ 0 ⇔ a - 2√ab +b ≥ 0 ⇔ a+b≥ 2√ab
dấu "=" xảy ra khi và chỉ khi a=b
vậy ta có dpcm
Áp dụng bất đẳng thức Cô-si với hai số dương a và b có:
\(\dfrac{a+b}{2}\ge\sqrt{ab}\)
\(\Rightarrow a+b\ge2\sqrt{ab}\left(\text{Đ}PCM\right)\)