Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: d//d1
=>m-2=-m và m+7<>2m-3
=>m=1
b: d trùng với d2
=>m-2=-m^2 và m+7=-2m+1
=>m=-2 và m^2+m-2=0
=>m=-2
d: d vuông góc d4
=>-1/6(m+3)(m-2)=-1
=>(m+3)(m-2)=6
=>m^2+m-6-6=0
=>m^2+m-12=0
=>m=-4 hoặc m=3
c: Thay y=1/3 vào d3, ta được:
-2/3x+5/3=1/3
=>-2/3x=-4/3
=>x=2
Thay x=2 và y=1/3 vào (d), ta được:
2(m-2)+m+7=1/3
=>3m+3=1/3
=>3m=-8/3
=>m=-8/9

a: 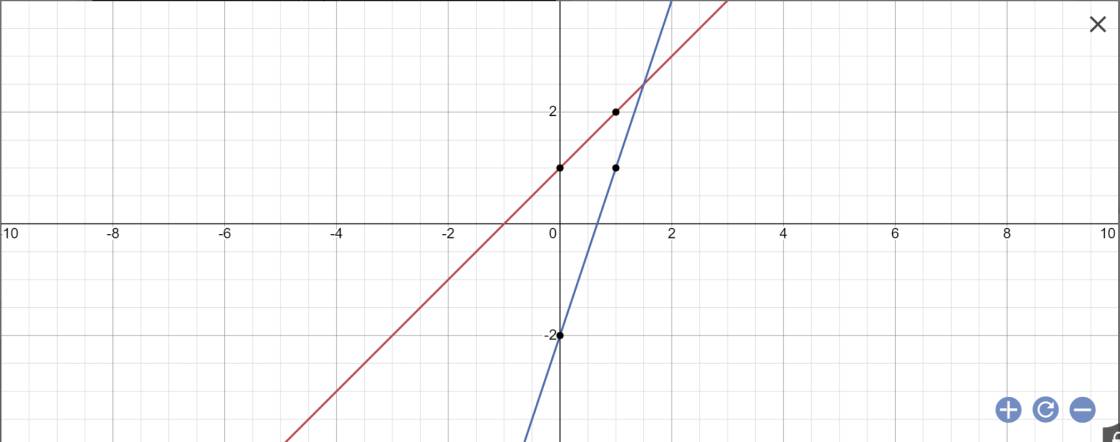
b: Tọa độ giao điểm của (d1) và (d2) là:
\(\left\{{}\begin{matrix}3x-2=x+1\\y=x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x-x=2+1\\y=x+1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x=3\\y=x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3}{2}\\y=\dfrac{3}{2}+1=\dfrac{5}{2}\end{matrix}\right.\)
Thay x=3/2 và y=5/2 vào (d3), ta được:
\(2m+3\cdot\dfrac{3}{2}-1=\dfrac{5}{2}\)
=>\(2m+\dfrac{7}{2}=\dfrac{5}{2}\)
=>\(2m=-1\)
=>m=-1/2
c: (d3): y=2m+3x-1
=>y=m*2+3x-1
Tọa độ điểm mà (d3) luôn đi qua là:
\(\left\{{}\begin{matrix}2=0\left(vôlý\right)\\y=3x-1\end{matrix}\right.\)
=>(d3) không đi qua cố định bất cứ điểm nào

Tọa độ giao điểm của (d1) và (d3) là:
\(\left\{{}\begin{matrix}2x-1=-x+3\\y=-x+3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3x=4\\y=-x+3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{4}{3}\\y=-\dfrac{4}{3}+3=\dfrac{5}{3}\end{matrix}\right.\)
Thay x=4/3 và y=5/3 vào (d2), ta được:
\(\dfrac{4}{3}\left(2n-1\right)+\dfrac{3}{2}=\dfrac{5}{3}\)
=>\(\dfrac{8}{3}n-\dfrac{4}{3}+\dfrac{3}{2}=\dfrac{5}{3}\)
=>\(\dfrac{8}{3}n=\dfrac{5}{3}+\dfrac{4}{3}-\dfrac{3}{2}=\dfrac{3}{2}\)
=>\(n=\dfrac{3}{2}:\dfrac{8}{3}=\dfrac{3}{2}\cdot\dfrac{3}{8}=\dfrac{9}{16}\)

d1xd2 : x +2 = -x -2 => 2x = -4 => x =-2 ; y =0 A( -2;0)
d2xd3 : -x -2 = -2x +2 => x = 4 => y= 6 B (4;6)
d1xd3 : x +2 = -2x +2 => 3x =0 => x =0 => y =2 C (0;2)
tính AB ; AC; BC sau đó dùng công thức Herong nhé .

Tọa độ giao điểm của (d2) và (d3) là nghiệm của hệ phương trình sau:
\(\left\{{}\begin{matrix}x+1=-x+3\\y=x+1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x=2\\y=x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)
Thay x=1 và y=2 vào (d1), ta được:
\(\left(m^2-1\right)+m^2-5=2\)
=>\(2m^2=8\)
=>\(m^2=4\)
=>\(\left[{}\begin{matrix}m=2\\m=-2\end{matrix}\right.\)

Bây giờ ta sẽ đi tìm tọa độ giao điểm của 3 đường thẳng trên
Với (d1) và (d2) cắt nhau tại điểm \(A\left(x_1;y_1\right)\) nên khi đó:
\(\hept{\begin{cases}y_1=3x_1-2\\y_1=-\frac{1}{3}x_1+\frac{4}{3}\end{cases}}\Rightarrow3x_1-2=-\frac{1}{3}x_1+\frac{4}{3}\Leftrightarrow\frac{10}{3}x_1=\frac{10}{3}\Rightarrow\hept{\begin{cases}x_1=1\\y_1=1\end{cases}}\)
Vậy \(A\left(1;1\right)\)
Tương tự gọi B,C là giao điểm của đường (d3) với (d2) , (d1)
Khi đó ta dễ dàng tính được: \(B\left(4;0\right)\) ; \(C\left(2;4\right)\)
Áp dụng công thức tính khoảng cách giữa 2 điểm trong mặt phẳng ta có:
\(AB=\sqrt{\left(1-4\right)^2+\left(1-0\right)^2}=\sqrt{10}\Rightarrow AB^2=10\)
\(AC=\sqrt{\left(1-2\right)^2+\left(1-4\right)^2}=\sqrt{10}\Rightarrow AC^2=10\)
\(BC=\sqrt{\left(4-2\right)^2+\left(0-4\right)^2}=\sqrt{20}\Rightarrow BC^2=20\)
Xét tam giác ABC có: \(\hept{\begin{cases}AB=AC\\AB^2+AC^2=BC^2\left(=20\right)\end{cases}}\)
=> Tam giác ABC vuông cân tại A
=> đpcm
giao điểm của d1 với d2 là : y=3x-2
y=-1/3x+4/3
<=> 3x -2 =-1/3+4/3
y=3x-2
<=> x=1
y=1
vaaky giao điểm của d1 và d2 có tọa độ A(1,1)
tương tự ta được giao điểm của: d2 với d3 có tọa độ B (4,0)
d3 với d1 có tọa độ C(2,4)
độ dài AB là\(\sqrt{\left(Xa-Xb\right)^2+\left(Ya+Yb\right)^2}\)=\(\sqrt{\left(1-4\right)^2+\left(1-0\right)^2}\)=\(\sqrt{10}\)
tương tư ta được AC= \(\sqrt{10}\)
=> AB=AC ; d1 vuông góc d2 vì 3.(-1/3)=-1
=> tam giác ABC VUÔNG CÂN