K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
CM
10 tháng 7 2017
a) Xét hàm số f(x) = tanx − sinx trên nửa khoảng [0; π/2);
x ∈ [0;1/2)
Dấu “=” xảy ra khi x = 0.
Suy ra f(x) đồng biến trên nửa khoảng [0; π/2)
Mặt khác, ta có f(0) = 0, nên f(x) = tanx – sinx > 0 hay tanx > sinx với mọi x ∈ [0; 1/2)
b) Xét hàm số h(x) trên [0; + ∞ )
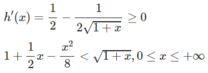
Dấu “=” xẩy ra chỉ tại x = 0 nên h(x) đồng biến trên nửa khoảng [0; + ∞ ).
Vì h(x) = 0 nên
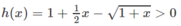
Hay
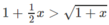
Xét hàm số trên f(x) trên [0; + ∞ );
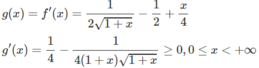
Vì g(0) = 0 và g(x) đồng biến trên nửa khoảng [0; + ∞ ) nên g(x) ≥ 0, tức là f′(x) ≥ 0 trên khoảng đó và vì dấu “=” xảy ra chỉ tại x = 0 nên f(x) đồng biến trên nửa khoảng .
Mặt khác, ta có f(0) = 0 nên
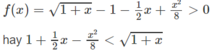
Với mọi 0 < x < + ∞ .
PT
1
CM
27 tháng 10 2017
Xét hàm số f(x) = tanx − sinx trên nửa khoảng [0; π /2);
x ∈ [0;1/2)
Dấu “=” xảy ra khi x = 0.
Suy ra f(x) đồng biến trên nửa khoảng [0; π /2)
Mặt khác, ta có f(0) = 0, nên f(x) = tanx – sinx > 0 hay tanx > sinx với mọi x ∈ [0; 1/2)
AH
Akai Haruma
Giáo viên
12 tháng 2 2022
Bạn cần viết đề bằng công thức toán (biểu tượng $\sum$ ở góc trái khung soạn thảo) để được hỗ trợ tốt hơn.
NY
1
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 8 2020
\(\Leftrightarrow\left|cosx\right|\ge cos^2x\)
\(\Leftrightarrow\left|cosx\right|-\left|cosx\right|^2\ge0\)
\(\Leftrightarrow\left|cosx\right|\left(1-\left|cosx\right|\right)\ge0\) (1)
Do \(0\le\left|cosx\right|\le1\Rightarrow1-\left|cosx\right|\ge0\) với mọi x
\(\Rightarrow\left(1\right)\) luôn đúng với mọi x (đpcm)
CM
27 tháng 2 2019
Ta có: a ∆ → = (2; 3; 2) và n α → = (2; −2; 1)
a ∆ → . n α → = 4 – 6 + 2 = 0 (1)
Xét điểm M 0 (-3; -1; -1) thuộc ∆ , ta thấy tọa độ M 0 không thỏa mãn phương trình của ( α ) . Vậy M 0 ∉ ( α ) (2).
Từ (1) và (2) ta suy ra ∆ // ( α ).
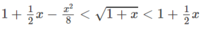
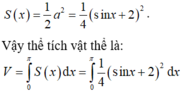
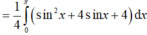
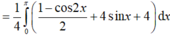
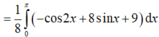
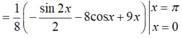
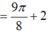
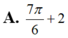
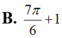
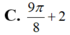
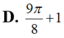
Xét hàm số \(f\left(x\right)=sinx+tanx-2x\left(0< x< \dfrac{\pi}{2}\right)\)
\(f'\left(x\right)=cosx+\dfrac{1}{cos^2x}-2\)
mà \(cosx>cos^2x\left(0< x< \dfrac{\pi}{2}\Rightarrow0< cosx< 1\right)\)
\(\Rightarrow f'\left(x\right)=cosx+\dfrac{1}{cos^2x}-2>cos^2x+\dfrac{1}{cos^2x}-2\)
mà \(cos^2x+\dfrac{1}{cos^2x}\ge2\sqrt[]{cos^2x.\dfrac{1}{cos^2x}}=2\left(Bđt.Cauchy\right)\)
\(\Rightarrow f'\left(x\right)>2-2=0\)
\(\Rightarrow f\left(x\right)\) đồng biến trên \(0< x< \dfrac{\pi}{2}\)
\(\Rightarrow f\left(x\right)>f\left(0\right)=0,\forall x\in\left(0;\dfrac{\pi}{2}\right)\)
\(\Rightarrow sinx+tanx-2x>0\)
\(\Rightarrow sinx+tanx>2x,\forall x\in\left(0;\dfrac{\pi}{2}\right)\)
\(\Rightarrow dpcm\)