Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

2.
\(\lim\limits_{x\rightarrow0^-}f\left(x\right)=\lim\limits_{x\rightarrow0^-}\left(x+2a\right)=2a\)
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^+}\left(x^2+x+1\right)=1\)
Hàm liên tục tại \(x=0\Leftrightarrow\lim\limits_{x\rightarrow0^-}f\left(x\right)=\lim\limits_{x\rightarrow0^+}f\left(x\right)\)
\(\Leftrightarrow2a=1\Rightarrow a=\dfrac{1}{2}\)
3. Đặt \(f\left(x\right)=x^4-x-2\)
Hàm \(f\left(x\right)\) liên tục trên R nên liên tục trên \(\left(1;2\right)\)
\(f\left(1\right)=-2\) ; \(f\left(2\right)=12\Rightarrow f\left(1\right).f\left(2\right)=-24< 0\)
\(\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc (1;2)
Hay pt đã cho luôn có nghiệm thuộc (1;2)

Hàm có đạo hàm tại \(x=0\) khi nó liên tục tại \(x=0\) và có đạo hàm trái bằng đạo hàm phải tại 0
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^+}\left(-x^3+bx+c\right)=c\)
\(\lim\limits_{x\rightarrow0^-}f\left(x\right)=\lim\limits_{x\rightarrow0^-}x^2=0\)
\(\Rightarrow c=0\)
\(f'\left(0^-\right)=2x_{x\rightarrow0^-}=0\)
\(f'\left(0^+\right)=\left(-3x^2+b\right)_{x\rightarrow0^+}=b\)
\(\Rightarrow b=0\Rightarrow b=c=0\)

\(\lim\limits_{x\rightarrow0}\left|f\left(x\right)\right|=\lim\limits_{x\rightarrow0}\left|x^2sin\dfrac{1}{x}\right|< \lim\limits_{x\rightarrow0}\left|x^2\right|=0\).
Vậy \(\lim\limits_{x\rightarrow0}f\left(x\right)=0\).
\(f\left(0\right)=A\).
Để hàm số liên tục tại \(x=0\) thì \(\lim\limits_{x\rightarrow0}f\left(x\right)=f\left(0\right)\Leftrightarrow A=0\).
Để xét hàm số có đạo hàm tại \(x=0\) ta xét giới hạn:
\(\lim\limits_{x\rightarrow0}\dfrac{f\left(x\right)-f\left(0\right)}{x-0}=\lim\limits_{x\rightarrow0}\dfrac{x^2sin\dfrac{1}{x}}{x}=\lim\limits_{x\rightarrow0}xsin\dfrac{1}{x}=0\).
Vậy hàm số có đạo hàm tại \(x=0\).

Để hàm số có đạo hàm tại 1 điểm thì nó phải liên tục tại điểm đó đồng thời đạo hàm trái bằng đạo hàm phải
\(\lim\limits_{x\rightarrow0^-}\left(2ax+1\right)=1\)
\(\lim\limits_{x\rightarrow0^+}\left(x^2+ax+1\right)=1\)
\(\Rightarrow\) Hàm liên tục tại \(x=1\)
\(y'\left(0^+\right)=2a\)
\(y'\left(0^-\right)=\left(2x+a\right)_{x=0^-}=a\)
Hàm có đạo hàm tại x=0 \(\Leftrightarrow2a=a\Leftrightarrow a=0\)

\(y = \left| x \right| = \left\{ \begin{array}{l}x\,\,\,(x \ge 0)\\ - x\,\,\,(x < 0)\end{array} \right. \Rightarrow y' = \left\{ \begin{array}{l}1\,\,\,(x \ge 0)\\ - 1\,\,\,(x < 0)\end{array} \right.\)
Ta có: \(\mathop {\lim }\limits_{x \to {0^ + }} y' = 1 \ne - 1 = \mathop {\lim }\limits_{x \to {0^ - }} y'\)
Vậy không tồn tại đạo hàm của hàm số tại x = 0

Lời giải:
Để hàm số trên liên tục tại $x_0=0$ thì:
\(\lim\limits_{x\to 0+}f(x)=\lim\limits_{x\to 0-}f(x)=f(0)\)
\(\Leftrightarrow \lim\limits_{x\to 0+}(a+\frac{4-x}{x+2})=\lim\limits_{x\to 0-}(\frac{\sqrt{1-x}+\sqrt{1+x}}{x})=a+2\)
\(\Leftrightarrow a+2=\lim\limits_{x\to 0-}\frac{\sqrt{1-x}+\sqrt{1+x}}{x}\)
Mà \(\lim\limits_{x\to 0-}\frac{\sqrt{1-x}+\sqrt{1+x}}{x}=-\infty \) nên không tồn tại $a$ để hàm số liên tục tại $x_0=0$

\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt{x+4}-2}{x}=\lim\limits_{x\rightarrow0^+}\dfrac{x}{x\left(\sqrt{x+4}+2\right)}=\lim\limits_{x\rightarrow0^+}\dfrac{1}{\sqrt{x+4}+2}=\dfrac{1}{4}\)
\(f\left(0\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)=\lim\limits_{x\rightarrow0^-}\left(mx^2+2m+\dfrac{1}{4}\right)=2m+\dfrac{1}{4}\)
Hàm liên tục tại x=0 khi: \(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)=f\left(0\right)\)
\(\Leftrightarrow2m+\dfrac{1}{4}=\dfrac{1}{4}\Leftrightarrow m=0\)


Ta có f(x) =
f(x) =  (x – 1)2 = 1 và
(x – 1)2 = 1 và 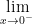 f(x) =
f(x) = 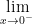 (-x2) = 0.
(-x2) = 0.
vì f(x) ≠
f(x) ≠ 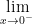 nên hàm số y = f(x) gián đoạn tại x = 0, do đó hàm số không có đạo hàm tại điểm x = 0.
nên hàm số y = f(x) gián đoạn tại x = 0, do đó hàm số không có đạo hàm tại điểm x = 0.
Ta có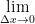
 =
= 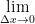
 =
= 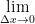 (2 + ∆x) = 2.
(2 + ∆x) = 2.
Vậy hàm số y = f(x) có đạo hàm tại x = 2 và f'(2) = 2.