Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(A=2x^2+x-x^3-2x^2+x^3-x+3=3\)=> k phụ thuộc vào biến
\(B=24-4x+2x^2+3x^3-5x^2+4x+3x^2-3x^3=24\)=> k phụ thuộc vào biến

a , x^2 - 2x - (3x^2 - 5x + 4) + (2x^2 - 3x + 7)
= x^2 - 2x - 3x^2 + 5x - 4 + 2x^2 - 3x + 7
= (x^2 - 3x^2 + 2x^2) + (-2x + 5x - 3x) + (-4 + 7)
= 3
Vậy GTBT ko phụ thuộc vào biến
b, (2x^3 - 4x^2 + x - 1) - (5 - x^2 + 2x^3) + 3x^2 - x
= 2x^3 - 4x^2 + x - 1 - 5 + x^2 - 2x^3 + 3x^2 - x
= (2x^3 - 2x^3) + (-4x^2 + x^2 + 3x^2 ) + (x - x) + (-1 - 5)
= -6
Vậy GTBT ko phụ thuộc vào biến
a) x2 -2x -( 3x2 -5x +4 )+(2x2 - 3x +7 )
= x2 -2x - 3x2 + 5x - 4 + 2x2 - 3x +7
= 3
Vậy biểu thức không phụ thuộc vào biến.
b) ( 2x3 -4x2 +x - 1)- (5 - x2 +2x3 ) +3x2 - x
= 2x3 -4x2 +x - 1 - 5 + x2 - 2x3 +3x2 - x
= -1 - 5 = -6
Vậy biểu thức không phụ thuộc vào biến x

a) x(2x+1)-x2(x+2)+(x3-x+3)= 2x2+x-x3-2x2+x3-x+3= 3
b)x (3x2-x+5)-(2x3+3x-16)-x(x2-x+2)= 3x3-x2+5x-2x3-3x+16-x3+x2-2x= 16

a) \(\left(x+2\right)\left(x^2+2x+4\right)-x\left(x^2+1\right)+x+2\)
\(=x^3+8-x^3-x+x+2\)
\(=10\)
Vậy giá trị của bt không phụ thuộc vào gt của biến
b) \(\left(3x-5\right)\left(2x+11\right)-\left(2x+3\right)\left(3x+7\right)\)
\(=6x^2+23x-55-6x^2-23x-21\)
\(=-76\)
Vậy gt của bt không phụ thuộc vào gt của biến

a)
x(2x + 1) - x2(x + 2) + (x3 - x + 3)
\(=2x^2+x-x^3-2x^2+x^3-x+3\)
\(=\left(x^3-x^3\right)+\left(2x^2-2x^2\right)+\left(x-x\right)+3\)
\(=3\)\(\left(ĐPCM\right)\)
b)
x(3x2 - x + 5) - (2x3 +3x - 16) - x(x2 - x + 2)
\(=3x^3-x^2+5x-2x^3-3x+16-x^3+x^2-2x\)
\(=\left(3x^3-2x^3-x^3\right)-\left(x^2-x^2\right)+\left(5x-3x-2x\right)+16\)
\(=16\left(ĐPCM\right)\)

a: \(=x^2-2x-3x^2+5x-4+2x^2-3x+7=3\)
b: \(=2x^3-4x^2+x-1-5+x^2-2x^3+3x^2-x=4\)
c: \(=1-x-\dfrac{3}{5}x^2-x^4+2x+6+0.6x^2+x^4-x=7\)
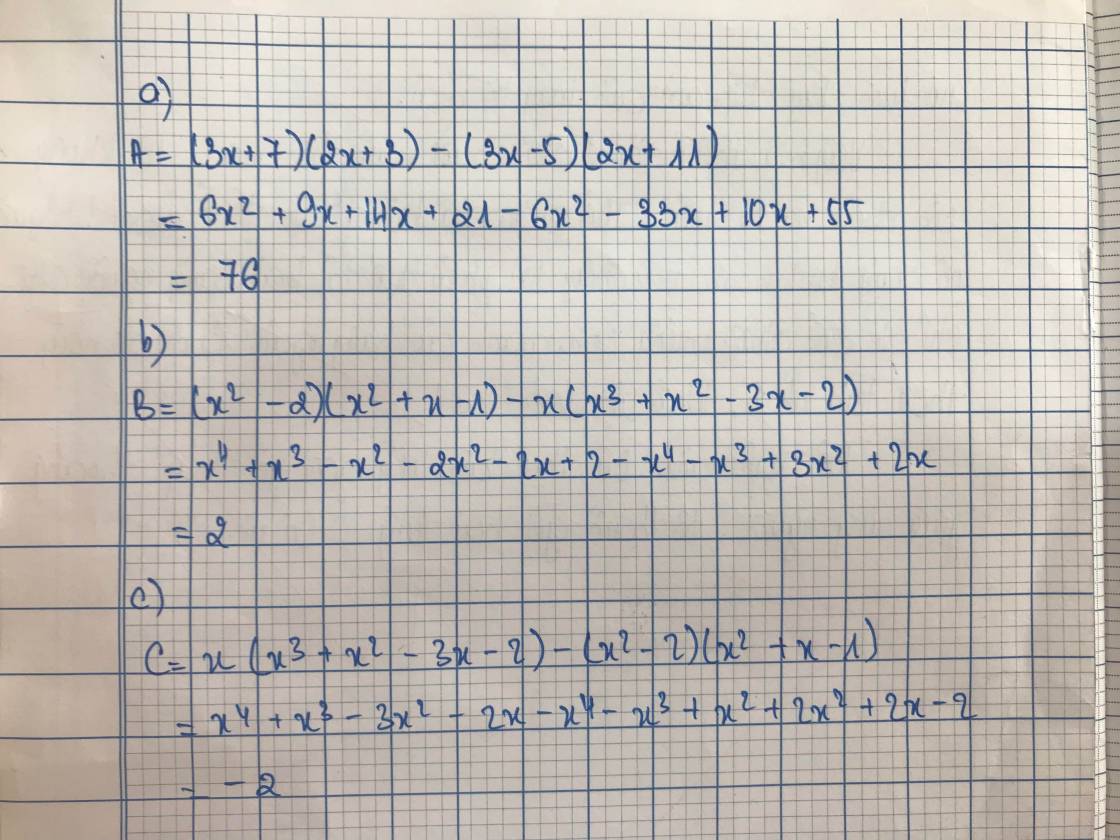
\(a,A=\left(x+6\right)^2+2\left(x-5\right)^2-\left(x+2\right)^2-2\left(x-3\right)^2\\ A=x^2+12x+36+2x^2-20x+50-x^2-4x-4-2x^2+12x-18\\ A=64\\ b,B=\left(x-2\right)\left(x^2+2x+4\right)-\left(x+2\right)\left(x^2-2x+4\right)=x^3-8-x^3-8=-16\)
a) \(A=\left(x+6\right)^2+2\left(x-5\right)^2-\left(x+2\right)^2-2\left(x-3\right)^2\)
\(=x^2+12x+36+2x^2-20x+50-x^2-4x-4-2x^2+12x-18\)
\(=64\)
b) \(B=x^3-8-x^3-8=-16\)