Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi O là giao điểm của AC và BD. Theo tính chất hình bình hành thì O là trung điểm AC và BD.
Gọi H, I, J, L lần lượt là chân các đường cao hạ từ D, O, C, B xuống đường thẳng xy.
Ta thấy ngay DH // OI // CJ // KB.
Xét tam giác ACJ có O là trung điểm AC, OI // CJ nên OI là đường trung bình tam giác hay CJ = 2OI. (1)
Xét hình thang vuông HDBK có O là trung điểm BD, OI // DH // BK nên OI là đường trung bình hình thang.
Vậy thì \(DH+BK=2OI\) (2)
Từ (1) và (2) suy ra CJ = DH + BK.
Suy ra \(\frac{1}{2}CJ.AE=\frac{1}{2}HD.AE+\frac{1}{2}BK.AE\) hay \(S_{ACE}=S_{ADE}+S_{ABE}\)
1
Ta có do \(K\in CD;CD//AB\Rightarrow\widehat{K1}=\widehat{A2}\)
Mà \(\widehat{A2}=\widehat{A1}\)(AK LÀ PHÂN GIÁC)
\(\Rightarrow\widehat{K1}=\widehat{A1}\Rightarrow\Delta ADK\)cân tại D => AD=DK
Tương tự ta cm được BC=CK
=> AD+BC=DK+CK
Mà K nằm giữa C và D nên AD+BC=DK+CK=DC(đpcm)

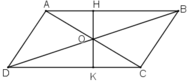
Gọi OH, OK lần lượt là chiều cao của tam giác AOB và tam giác DOC.
Ta có: OK ⊥ CD, CD // AB ⇒ OK ⊥ AB ⇒ O, H, K thẳng hàng.
Do đó:
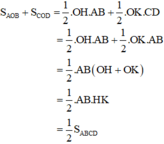
Mà SABCD = SAOB + SBOC + SCOD + SDOA

Do đó SAOB + SCOD = SBOC + SDOA.

Qua O vẽ OH ⊥ AB và OK ⊥ AD ⇒ OH ⊥ DC, OK ⊥ BC
Gọi I, L lần lượt là giao điểm của OK, OH với DC, BC. Ta có:
+ S_ABCD = AB.IH = BC.KL
+ S_ABO = 1/2 AB.OH và S_CDO = 1/2 DC.OI
⇒ S_ABO + S_CDO = 1/2 AB.OH + 1/2 DC.OI
= 1/2 AB.OH + 1/2 AB.OI
= 1/2 AB (OH + OI) = 1/2 AB.IH = 1/2 S_ABCD (1)
+ S_BCO = 1/2 BC.OL và S_DAO = 1/2 AD.OK
⇒ S_BCO + SDAO = 1/2 BC.OL + 1/2AD.OK
= 1/2 BC.OL + 1/2BC.OK
= 1/2BC(OL + OK) = 1/2 BC.KL = 1/2S_ABCD (2)
Từ (1) và (2) ta có: S_ABO + S_CDO = S_BCO + S_DAO

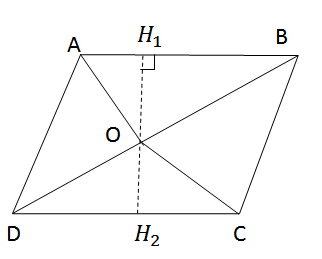
Từ O lẻ đường thẳng d vuông góc với AB ở H1, cắt CD ở H2.
Ta có OH1 ⊥ AB
Mà AB // CD
Nên OH2 ⊥ CD
Do đó: SABO + SCDO = \(\dfrac{1}{2}\)OH1 . AB + \(\dfrac{1}{2}\) OH2 . CD
= \(\dfrac{1}{2}\)AB (OH1 + OH2)
= \(\dfrac{1}{2}\)AB . H1 . H2
Nên \(S_{ABO}+S_{CDO}=\dfrac{1}{2}S_{ABCD}\) ( 1)
Tương tự \(S_{BCO}+S_{DAO}=\dfrac{1}{2}S_{ABCD}\) (2)
Từ (1) và (2) suy ra :
\(S_{ABO}+S_{CDO}=S_{BCO}+S_{DAO}\)