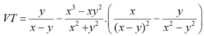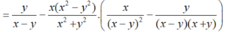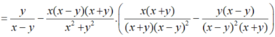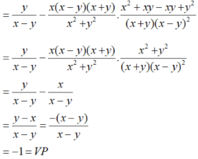Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


`x^2 -4x+4-y^2`
`=(x^2 -4x+4)-y^2`
`=(x-2)^2 -y^2`
`=(x-2-y)(x-2+y)`
`x^2+2xy+y^2-x-y`
`=(x^2+2xy+y^2) -(x+y)`
`=(x+y)^2 -(x+y)`
`=(x+y)(x+y-1)`
`x^2-2xy+y^2-9`
`=(x^2-2xy+y^2)-3^2`
`=(x-y)^2-3^3`
`=(x-y-3)(x-y+3)`
Tách ra đi cậu.


Lời giải:
$P=(x+1)^3-(x+1)^3-[(x-1)^2+(x+1)^2]$
$=-[(x-1)^2+(x+1)^2]=-[(x^2-2x+1)+(x^2+2x+1)]=-2(x^2+1)$ phụ thuộc vào giá trị của biến nhé. Bạn xem lại đề.
$Q=(2x)^3-y^3+(2x)^3+y^3-16x^3$
$=8x^3-y^3+8x^3+y^3-16x^3=(8x^3+8x^3-16x^3)+(-y^3+y^3)=0+0=0$ không phụ thuộc vào giá trị của biến (đpcm)

\(x^2-xy+y^2=x^2-2.x.\frac{1}{2}y+\left(\frac{1}{2}y\right)^2+\frac{3y^2}{4}\)\(=\left(x-\frac{1}{2}y\right)^2+\frac{3y^2}{4}\ge0\) với mọi x,y.

\(A=x^2+2y^2-2xy-2y+15\)
\(=\left(x^2+2xy+y^2\right)+\left(y^2-2y+1\right)+14>14>0\)
Vậy : \(A>0\)

Ta có:
x2 – 2xy + y2 + 1
= (x2 – 2xy + y2) + 1
= (x – y)2 + 1.
(x – y)2 ≥ 0 với mọi x, y ∈ R
⇒ x2 – 2xy + y2 + 1 = (x – y)2 + 1 ≥ 0 + 1 = 1 > 0 với mọi x, y ∈ R (ĐPCM).