
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét VT :\(\left(4-\sqrt{7}\right)^2=14-8\sqrt{7}+7=23-8\sqrt{7}\)
=> VT=VP ( đpcm)

a) \(9+4\sqrt{5}=4+4\sqrt{5}+5=2^2+2\cdot2\sqrt{5}+\left(\sqrt{5}\right)^2=\left(\sqrt{5}+2\right)^2\left(ĐPCM\right)\)
a) \(9+4\sqrt{5}=\left(\sqrt{5}\right)^2+2.\sqrt{5}.2+2^2=\left(\sqrt{5}+2\right)^2\left(đpcm\right)\)
b)\(\sqrt{9-4\sqrt{5}}-\sqrt{5}=\sqrt{\left(\sqrt{5}-2\right)^2}-\sqrt{5}=\sqrt{5}-2-\sqrt{5}=-2\left(đpcm\right)\)
c)\(\left(4-\sqrt{7}\right)^2=16-8\sqrt{7}+7=23-8\sqrt{7}\left(đpcm\right)\)
d)\(\sqrt{23+8\sqrt{7}}-\sqrt{7}=\sqrt{\left(4+\sqrt{7}\right)^2}-\sqrt{7}=4+\sqrt{7}-\sqrt{7}=4\left(đpcm\right)\)

\(\left(4-\sqrt{7}\right)^2=4^2-2\cdot4\cdot\sqrt{7}+7\)
\(=16-8\sqrt{7}+7=23-8\sqrt{7}\)
\(\sqrt{9-4\sqrt{5}}-\sqrt{5}\)
\(=\sqrt{5-2\cdot\sqrt{5}\cdot2+4}-\sqrt{5}\)
\(=\sqrt{\left(\sqrt{5}-2\right)^2}-\sqrt{5}\)
\(=\left|\sqrt{5}-2\right|-\sqrt{5}\)
\(=\sqrt{5}-2-\sqrt{5}=-2\)
\(\dfrac{\sqrt{4-2\sqrt{3}}}{1+\sqrt{2}}:\dfrac{\sqrt{2}-1}{\sqrt{3}+1}\)
\(=\dfrac{\sqrt{3-2\cdot\sqrt{3}\cdot1+1}}{\sqrt{2}+1}\cdot\dfrac{\sqrt{3}+1}{\sqrt{2}-1}\)
\(=\dfrac{\sqrt{\left(\sqrt{3}-1\right)^2}}{\sqrt{2}+1}\cdot\dfrac{\sqrt{3}+1}{\sqrt{2}-1}\)
\(=\dfrac{\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)}{\left(\sqrt{2}+1\right)\left(\sqrt{2}-1\right)}=\dfrac{3-1}{2-1}=2\)
\(\left(\dfrac{2\sqrt{3}-\sqrt{6}}{\sqrt{8}-2}-\dfrac{\sqrt{216}}{3}\right)\cdot\dfrac{1}{\sqrt{6}}\)
\(=\left(\dfrac{\sqrt{6}\left(\sqrt{2}-1\right)}{2\left(\sqrt{2}-1\right)}-\dfrac{6\sqrt{6}}{3}\right)\cdot\dfrac{1}{\sqrt{6}}\)
\(=\left(\dfrac{1}{2}\sqrt{6}-2\sqrt{6}\right)\cdot\dfrac{1}{\sqrt{6}}\)
\(=\dfrac{1}{2}-2=-\dfrac{3}{2}=-1,5\)

- \(\sqrt{\sqrt{5}^2-2.2\sqrt{5}+4}-\sqrt{5}=\sqrt{\left(\sqrt{5}-2\right)^2}-\sqrt{5}=\sqrt{5}-2-\sqrt{5}=-2\left(dpcm\right)\)
- \(\sqrt{23+8\sqrt{7}}-\sqrt{7}=\sqrt{\sqrt{7}^2+2.4\sqrt{7}+16}-\sqrt{7}\)\(=\sqrt{\left(\sqrt{7}+4\right)^2}-\sqrt{7}=\sqrt{7}+4-\sqrt{7}=4\left(DPCM\right)\)

\(M=3^5+3^6+3^7\)
\(=3^5\left(1+3+3^2\right)=3^5.13⋮13\)
Bài này mà bạn bảo của lớp 9 á

a. 9+4\(\sqrt{5}\)=(\(\sqrt{5}\)+2)2
VT: 9+4\(\sqrt{5}\)=2\(^2\)+2.2.\(\sqrt{5}\)+(\(\sqrt{5}\))\(^2\)=(2+\(\sqrt{5}\))\(^2\)=VP
b. \(\sqrt{23+8\sqrt{7}}\)-\(\sqrt{7}\)=4
\(\Leftrightarrow\)\(\sqrt{4^2+2.4\sqrt{7}+\left(\sqrt{7}\right)^2}\)-\(\sqrt{7}\)=4
\(\Leftrightarrow\)\(\sqrt{4+\sqrt{7}}^2\)-\(\sqrt{7}\)=4
\(\Leftrightarrow\)4+\(\sqrt{7}\)-\(\sqrt{7}\)=4
\(\Leftrightarrow\)4=4
\(\Rightarrow\)VT=VP
\(\sqrt{5}\)\(\sqrt{5}\)
Cái dòng \(\sqrt{5}\)\(\sqrt{5}\) máy mình bị lỗi nên đánh thừa thông cảm nha.

a,\(\sqrt{23-8\sqrt{7}}-\sqrt{7}=\sqrt{16-8\sqrt{7}+7}-\sqrt{7}=\sqrt{\left(4-\sqrt{7}\right)^2}-\sqrt{7}=\left|4-\sqrt{7}\right|-\sqrt{7}=4-\sqrt{7}-\sqrt{7}=4\)
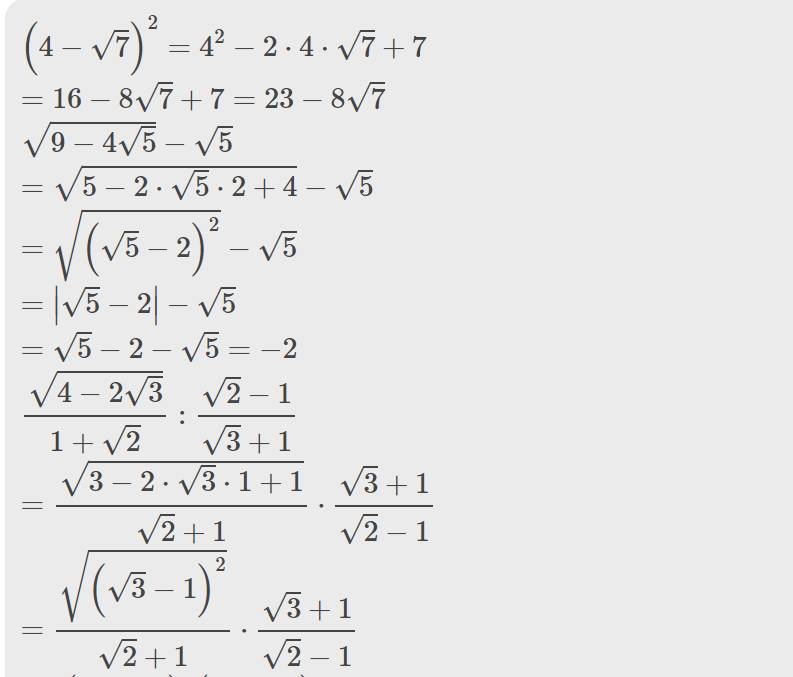
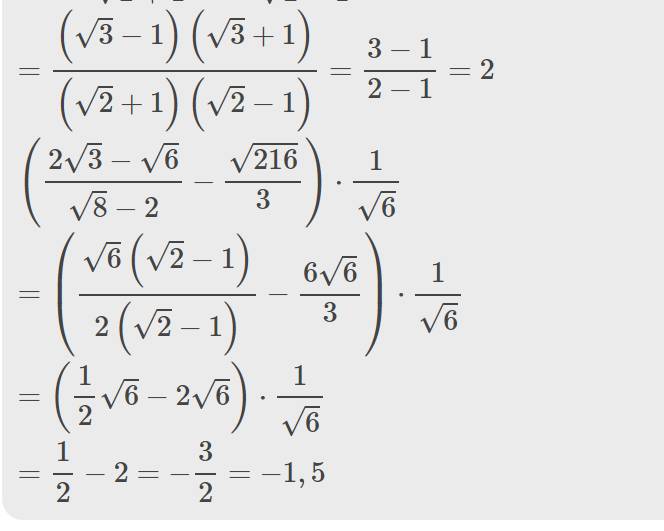
\(\left(4-\sqrt{7}\right)^2=4^2-2\cdot4\cdot\sqrt{7}+7=23-8\sqrt{7}\)