HT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 4 2022
Đề bài sai, ví dụ: với \(a=b=1\) thì \(x^2+x-1=0\) có 1 nghiệm thuộc \(\left(0;1\right)\) thỏa mãn yêu cầu
Nhưng \(x^2-2x+1=0\) có nghiệm kép, không phải hai nghiệm phân biệt
PL
1
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 3 2023
Đặt \(f\left(x\right)=\left(m^2-m+1\right)x^4-3x^3-1\)
\(f\left(x\right)\) là hàm đa thức nên liên tục trên mọi khoảng trên R
\(f\left(0\right)=-1< 0\)
\(f\left(3\right)=81\left(m^2-m+1\right)-55=81\left(m-\dfrac{1}{2}\right)^2+\dfrac{23}{4}>0\)
\(\Rightarrow f\left(0\right).f\left(3\right)< 0\Rightarrow\) pt có ít nhất 1 nghiệm thuộc \(\left(0;3\right)\)
\(f\left(-1\right)=m^2-m+2=\left(m-\dfrac{1}{2}\right)^2+\dfrac{7}{4}>0\)
\(\Rightarrow f\left(-1\right).f\left(0\right)< 0\Rightarrow\) pt có ít nhất 1 nghiệm thuộc \(\left(-1;0\right)\)
\(\Rightarrow\) Pt có ít nhất 2 nghiệm thuộc \(\left(-1;3\right)\Rightarrow\) có ít nhất 2 nghiệm trên \(\left(-5;5\right)\)
17 tháng 5 2016
a) Hàm số f(x) = 2x3 + 6x + 1 là hàm đa thức nên liên tục trên R.
Mặt khác vì f(0).f(1) = 1.(-3) < 0 nên phương trình có nghiệm trong khoảng (1; 2).
Vậy phương trình f(x) = 0 có ít nhất hai nghiệm.
b) Hàm số g(x) = cosx - x xác định trên R nên liên tục trên R.
Mặt khác, ta có g(0).g() = 1. (-
) < 0 nên phương trình đã cho có nghiệm trong khoảng (0;
).
SG
2
MH
4 tháng 4 2017
a) Hàm số f(x) = 2x3 + 6x + 1 là hàm đa thức nên liên tục trên R.
Mặt khác vì f(0).f(1) = 1.(-3) < 0 nên phương trình có nghiệm trong khoảng (1; 2).
Vậy phương trình f(x) = 0 có ít nhất hai nghiệm.
b) Hàm số g(x) = cosx – x xác định trên R nên liên tục trên R.
Mặt khác, ta có g(0).g(π/2) = 1. (-π/2) < 0 nên phương trình đã cho có nghiệm trong khoảng (0; π/2).
MT
4 tháng 4 2017
a) Hàm số f(x) = 2x3 + 6x + 1 là hàm đa thức nên liên tục trên R.
Mặt khác vì f(0).f(1) = 1.(-3) < 0 nên phương trình có nghiệm trong khoảng (1; 2).
Vậy phương trình f(x) = 0 có ít nhất hai nghiệm.
b) Hàm số g(x) = cosx - x xác định trên R nên liên tục trên R.
Mặt khác, ta có g(0).g() = 1. (-
) < 0 nên phương trình đã cho có nghiệm trong khoảng (0;
).
PT
1
CM
22 tháng 3 2018
Chứng minh rằng phương trình sau có ít nhất hai nghiệm :
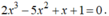
- Xét hàm số: f ( x ) = 2 x 3 - 5 x 2 + x + 1 là hàm đa thức.
⇒ Hàm số f liên tục trên R.
- Ta có:
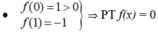có ít nhất một nghiệm c1 ∈ (0;1).
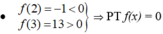có ít nhất một nghiệm c2 ∈ (2;3).
- Mà c ≠ c 2 nên PT f(x) = 0 có ít nhất 2 nghiệm.
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 3 2021
Xét hàm \(f\left(x\right)=m\left(x-1\right)^3\left(x^2-4\right)+x^4-3\)
Hàm \(f\left(x\right)\) là hàm liên tục trên R
\(f\left(1\right)=-2< 0\)
\(f\left(-2\right)=13>0\)
\(\Rightarrow f\left(x\right)=0\) luôn có ít nhất 1 nghiệm thuộc \(\left(-2;1\right)\)
\(f\left(2\right)=13>0\Rightarrow f\left(1\right).f\left(2\right)< 0\)
\(\Rightarrow f\left(x\right)=0\) luôn có ít nhất 1 nghiệm thuộc \(\left(1;2\right)\)
\(\Rightarrow\) Phương trình đã cho luôn có ít nhất 2 nghiệm với mọi m
Chắc bạn ghi nhầm đề, pt này giải luôn được mà:
\(x^{2018}-2018=0\Leftrightarrow x^{2018}=2018\)
\(\Leftrightarrow x=\pm\sqrt[2018]{2018}\)
Phương trình có đúng 2 nghiệm