K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
14 tháng 1 2017
a) Nếu ABC là một tam giác cân thì ABC là tam giác đều
Đây là mệnh đề sai
b) Nếu ABC là một tam giác cân và có một góc bằng 60o thì ABC là một tam giác đều
Đây là mệnh đề đúng

CM
27 tháng 8 2018
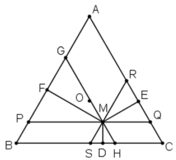
Ta có:
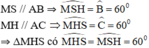
⇒ ΔMHS đều.
MD ⊥ SH nên MD là đường cao đồng thời là trung tuyến của ΔMHS.
⇒ D là trung điểm của HS
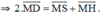
Chứng minh tương tự ta có:
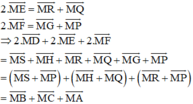
(Vì các tứ giác BSMP, HMQC, MRAG là hình bình hành)
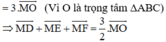

CM
15 tháng 2 2019
Đáp án: D
a sai vì nếu tam giác ABC thỏa mãn AB2 + AC2 = BC2 thì tam giác ABC vuông tại A không phải vuông tại B.
b, c, d đúng.
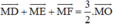
Xét tam giác ABC không phải tam giác đều
Nếu không có góc nào nhỏ hơn 60 độ thì ta có :
\(\widehat{A}+\widehat{B}+\widehat{C}\ge60^0+60^0+60^0\ge180^0\)
dấu bằng chỉ xảy ra khi cả ba góc bằng 60 độ mâu thuẫn với giả thiết ABC không phải tam giác đều
vậy phải có ít nhất một góc nhỏ hơn 60 độ
Xét tam giác ABCABC không phải tam giác đều.
Không mất tính tổng quát, có thể giả sử \(\widehat{A}\) ≥ \(\widehat{B}\) ≥ \(\widehat{C}\)
Vì tam giác ABC không phải là tam giác đều nên \(\widehat{A}\) > \(\widehat{C}\)
Giả sử \(\widehat{C}\) ≥ 60o thì \(\widehat{A}\) + \(\widehat{B}\) + \(\widehat{C}\) > 180o vô lý)
Do đó \(\widehat{C}\) < 60o nên một tam giác không phải là tam giác đều thì có ít nhất một góc nhọn nhỏ hơn 60o
\widehat{A} \ge \widehat{B} \ge \widehat{C}