Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi góc xOz, góc zOy là 2 góc kề bù ; và tia Ou, Ov lần lượt là tia phân giác của góc xOz, zOy.
* Để chứng minh 2 tia phân giác của 2 góc kề bù vuông góc với nhau, ta sẽ chứng minh tia Ou vuông góc tia Ov.
* Vì tia Ou, Ov lần lượt là tia phân giác của góc xOz, zOy
nên:
{ góc uOz = 1/2 góc xOz
{ góc zOv = 1/2 góc zOy
Suy ra:
{ 2 góc uOz = góc xOz
{ 2 góc zOv = góc zOy
Ta lại có:
góc xOz + góc zOy = 180 độ (vì 2 góc xOz, góc zOy kề bù)
=> 2 góc uOz + 2 góc zOv = 180 độ
=> 2(góc uOz + góc zOv) = 180 độ
=> góc uOz + góc zOv = 90 độ
=> góc uOv = 90 độ (vì 2 góc uOz, góc zOv kề nhau)
=> Tia Ou vuông góc Tia Ov
Do đó, 2 tia phân giác của 2 góc kề bù thì vuông góc với nhau.

Giả sử góc xOy bẹt, tia Oz và Om,On lần lượt là phân giác góc xOz và yOz
\(\Rightarrow\widehat{mOn}=\widehat{mOz}+\widehat{zOn}=\dfrac{1}{2}\widehat{xOz}+\dfrac{1}{2}\widehat{yOz}=\dfrac{1}{2}\left(\widehat{xOz}+\widehat{yOz}\right)=\dfrac{1}{2}\cdot\widehat{xOy}=\dfrac{1}{2}\cdot180^0=90^0\)
Do đó Om vuông góc On
Suy ra đpcm

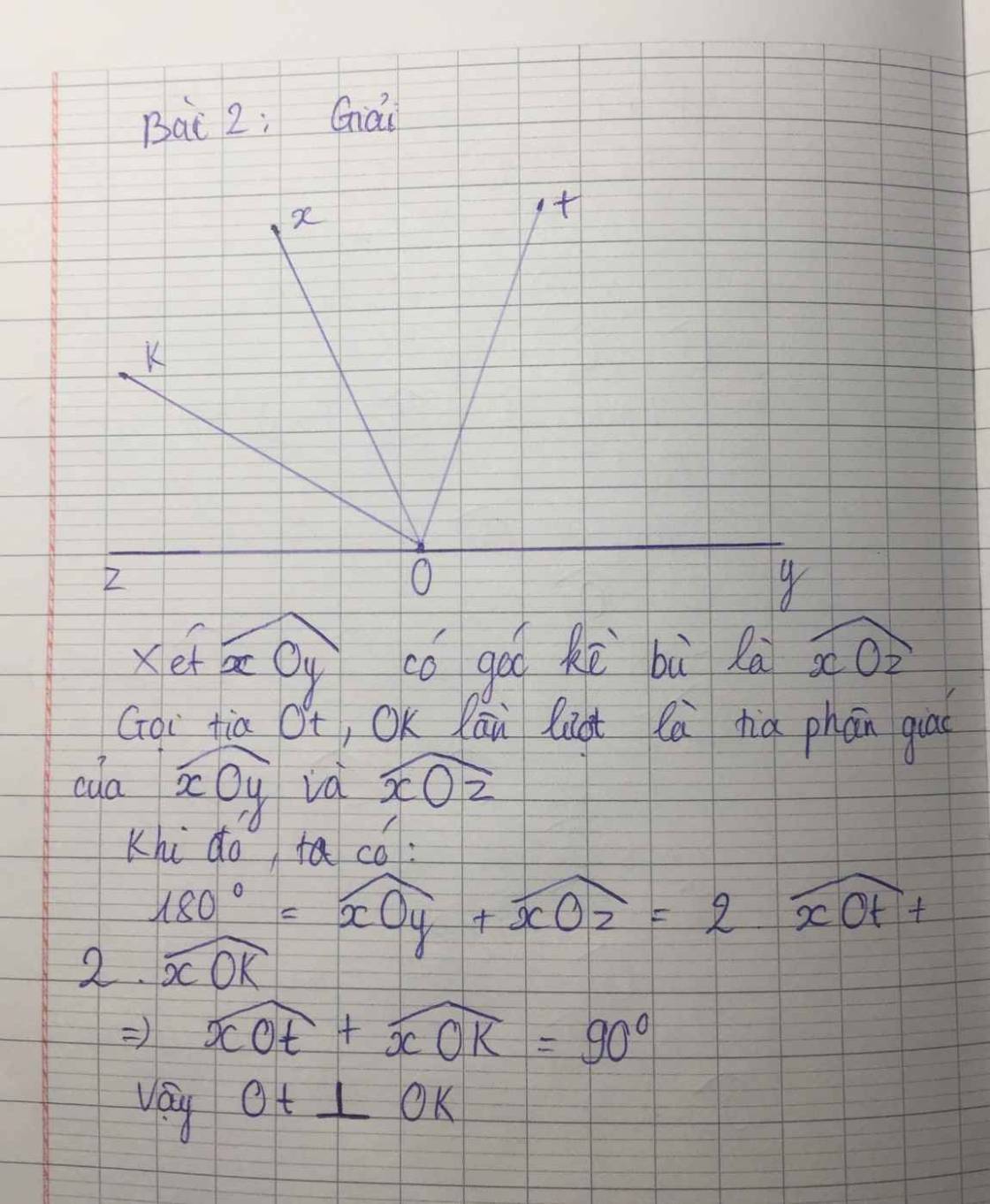
Như hình vẽ trên: DE là pg góc ADB và DF là pg góc ADC
=>ADE = 1/2 (ADB) và ADF = 1/2(ADC)
=>ADE + ADF = EDF = 1/2(ADB + ADC) = 1/2*180 = 90
=>dpcm
Giải:
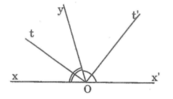
Đặt \(\widehat{xOy}=m^0(0< m^0< 180^0)\)
Hai góc xOy và yOx' là hai góc kề bù nên \(\widehat{xOy}+\widehat{yOx'}=180^0\)do đó \(\widehat{x'Oy}=180^0-\widehat{xOy}=180^0-m^0\)
Theo giả thiết Ot và Ot' lần lượt là tia phân giác của góc xOy và x'Oy nên \(\widehat{tOy}=\frac{1}{2}\widehat{xOy}=\frac{1}{2}m^0\)và \(\widehat{t'Oy}=\frac{1}{2}\widehat{x'Oy}=\frac{1}{2}\left[180^0-m^0\right]\). Tia Oy nằm giữa hai tia Ot và Ot', do đó \(\widehat{tOt}=\widehat{tOy}+\widehat{yOt'}=\frac{1}{2}m^0+\frac{1}{2}\left[180^0-m^0\right]=90^0\)
Vậy \(Ot\perp Ot'\)