Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(C=\left(x^2-1\right)\left(x^2+1\right)\left(x^4+1\right)\left(x^8+1\right)\left(x^{16}+1\right)\left(x^{32}+1\right)-x^{64}\\ =\left(x^4-1\right)\left(x^4+1\right)\left(x^8+1\right)\left(x^{16}+1\right)\left(x^{32}+1\right)-x^{64}\\ =\left(x^8-1\right)\left(x^8+1\right)\left(x^{16}+1\right)\left(x^{32}+1\right)-x^{64}\\ =\left(x^{16}-1\right)\left(x^{16}+1\right)\left(x^{32}+1\right)-x^{64}\\ =\left(x^{32}-1\right)\left(x^{32}+1\right)-x^{64}\\ =\left(x^{64}-1\right)-x^{64}\\ =-1\)
Vậy đa thức ko phụ thuộc vào x
\(C=(x^2-1)(x^2+1)(x^4+1)(x^8+1)(x^{16}+1)(x^{32}+1)-x^{64}\\=(x^4-1)(x^4+1)(x^8+1)(x^{16}+1)(x^{32}+1)-x^{64}\\=(x^8-1)(x^8+1)(x^{16}+1)(x^{32}+1)-x^{64}\\=(x^{16}-1)(x^{16}+1)(x^{32}+1)-x^{64}\\=(x^{32}-1)(x^{32}+1)-x^{64}\\=x^{64}-1-x^{64}\\=-1\)
⇒ Giá trị của C không phụ thuộc vào giá trị của biến

b: \(=\dfrac{2x^4-2x^3-2x^2-3x^3+3x^2+3x+x^2-x-1}{x^2-x-1}\)
\(=2x^2-3x+1\)

A(x)=(1-x^n)(1+x^n)/(1-x)(1+x)
B(x)=1-x^n/1-x
A(x) chia hết cho B(x) khi 1-x^n chia hết cho 1+x
x^n+1/x+1=A(x)+(1+(-1)^n)/(x+1)
=>1-x^n chia hết cho 1+x khi và chỉ khi n=2k+1

\(=x^3\left(x+2\right)-x\left(x+2\right)\)
\(=\left(x+2\right)\cdot x\cdot\left(x+1\right)\left(x-1\right)\)
Vì đây là tích của bốn số nguyên liên tiếp
nên \(\left(x+2\right)\cdot x\cdot\left(x+1\right)\cdot\left(x-1\right)⋮24\)

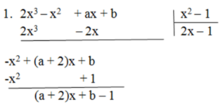
A(x) chia hết cho B(x) khi (a + 2)x + b – 1 là đa thức 0
Vậy a + 2 = 0 và b – 1 = 0 ⇒ a = -2 và b = 1

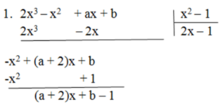
A(x) chia hết cho B(x) khi (a + 2)x + b – 1 là đa thức 0
Vậy a + 2 = 0 và b – 1 = 0 ⇒ a = -2 và b = 1
