Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
\(S_1=\dfrac{1}{1.5}=\dfrac{1}{5}\)
\(S_2=\dfrac{1}{1.5}+\dfrac{1}{5.9}=\dfrac{1}{4}\left(\dfrac{1}{1}-\dfrac{1}{5}\right)+\dfrac{1}{4}\left(\dfrac{1}{5}-\dfrac{1}{9}\right)\)
\(=\dfrac{1}{4}\left(1-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{9}\right)=\dfrac{1}{4}\left(1-\dfrac{1}{9}\right)=\dfrac{2}{9}\).
\(S_3=\dfrac{1}{1.5}+\dfrac{1}{5.9}+\dfrac{1}{9.13}=\dfrac{1}{4}\left(1-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{13}\right)\)
\(=\dfrac{1}{4}\left(1-\dfrac{1}{13}\right)=\dfrac{3}{13}\).
\(S_4=\dfrac{1}{1.5}+\dfrac{1}{5.9}+\dfrac{1}{9.13}+\dfrac{1}{13.17}\)\(=\dfrac{1}{4}\left(1-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{13}+\dfrac{1}{13}-\dfrac{1}{17}\right)\)
\(=\dfrac{1}{4}\left(1-\dfrac{1}{17}\right)=\dfrac{4}{17}\).
b) Dự đoán công thức : \(S_n=\dfrac{1}{4}\left(1-\dfrac{1}{4n+1}\right)\).
Chứng minh bằng quay nạp:
Với \(n=1\): \(S_1=\dfrac{1}{1.5}=\dfrac{1}{5}\).
Vậy giả thiết quy nạp đúng với n = 1.
Giả sử điều cần chứng minh đúng với \(n=k\).
Nghĩa là: \(S_k=\dfrac{1}{4}\left(1-\dfrac{1}{4k+1}\right)\).
Ta sẽ chứng minh nó đúng với \(n=k+1\): \(S_{k+1}=\dfrac{1}{4}\left(1-\dfrac{1}{4\left(k+1\right)+1}\right)\)
Thật vậy:
\(S_{k+1}=S_k+\dfrac{1}{\left[4\left(k+1\right)-3\right].\left[4\left(k+1\right)+1\right]}\)
\(=\dfrac{1}{4}\left(1-\dfrac{1}{4k+1}\right)+\dfrac{1}{4}\left(\dfrac{1}{4\left(k+1\right)-3}-\dfrac{1}{4\left(k+1\right)+1}\right)\)
\(=\dfrac{1}{4}\left(1-\dfrac{1}{4k+1}\right)+\dfrac{1}{4}\left(\dfrac{1}{4k+1}-\dfrac{1}{4\left(k+1\right)+1}\right)\)
\(=\dfrac{1}{4}\left(1-\dfrac{1}{4\left(k+1\right)+1}\right)\).
Vậy điều cần chứng minh đúng với mọi n.

a) Ta có:
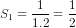
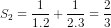
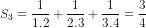
b) Từ câu a) ta dự đoán 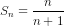 (1), với mọi n ε N* .
(1), với mọi n ε N* .
Ta sẽ chứng minh đẳng thức (1) bằng phương pháp quy nạp
Khi n = 1, vế trái là 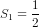 , vế phải bằng
, vế phải bằng 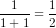 . Vậy đẳng thức (1) đúng.
. Vậy đẳng thức (1) đúng.
Giả sử đẳng thức (1) đúng với n = ≥ 1, tức là
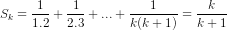
Ta phải chứng minh nó cũng đúng khi n = k + 1, nh=ghĩa là phải chứng minh
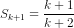
Ta có 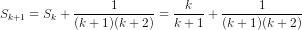
= 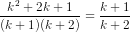
tức là đẳng thức (1) cũng đúng với n = k + 1.
Vậy điều cần chứng minh đúng với mọi n.

b)
Với n = 1.
\(VT=B_n=1;VP=\dfrac{1\left(1+1\right)\left(1+2\right)}{6}=1\).
Vậy với n = 1 điều cần chứng minh đúng.
Giả sử nó đúng với n = k.
Nghĩa là: \(B_k=\dfrac{k\left(k+1\right)\left(k+2\right)}{6}\).
Ta sẽ chứng minh nó đúng với \(n=k+1\).
Nghĩa là:
\(B_{k+1}=\dfrac{\left(k+1\right)\left(k+1+1\right)\left(k+1+2\right)}{6}\)\(=\dfrac{\left(k+1\right)\left(k+2\right)\left(k+3\right)}{6}\).
Thật vậy:
\(B_{k+1}=B_k+\dfrac{\left(k+1\right)\left(k+2\right)}{2}\)\(=\dfrac{k\left(k+1\right)\left(k+2\right)}{6}+\dfrac{\left(k+1\right)\left(k+2\right)}{2}\)\(=\dfrac{\left(k+1\right)\left(k+2\right)\left(k+3\right)}{6}\).
Vậy điều cần chứng minh đúng với mọi n.
c)
Với \(n=1\)
\(VT=S_n=sinx\); \(VP=\dfrac{sin\dfrac{x}{2}sin\dfrac{2}{2}x}{sin\dfrac{x}{2}}=sinx\)
Vậy điều cần chứng minh đúng với \(n=1\).
Giả sử điều cần chứng minh đúng với \(n=k\).
Nghĩa là: \(S_k=\dfrac{sin\dfrac{kx}{2}sin\dfrac{\left(k+1\right)x}{2}}{sin\dfrac{x}{2}}\).
Ta cần chứng minh nó đúng với \(n=k+1\):
Nghĩa là: \(S_{k+1}=\dfrac{sin\dfrac{\left(k+1\right)x}{2}sin\dfrac{\left(k+2\right)x}{2}}{sin\dfrac{x}{2}}\).
Thật vậy từ giả thiết quy nạp ta có:
\(S_{k+1}-S_k\)\(=\dfrac{sin\dfrac{\left(k+1\right)x}{2}sin\dfrac{\left(k+2\right)x}{2}}{sin\dfrac{x}{2}}-\dfrac{sin\dfrac{kx}{2}sin\dfrac{\left(k+1\right)x}{2}}{sin\dfrac{x}{2}}\)
\(=\dfrac{sin\dfrac{\left(k+1\right)x}{2}}{sin\dfrac{x}{2}}.\left[sin\dfrac{\left(k+2\right)x}{2}-sin\dfrac{kx}{2}\right]\)
\(=\dfrac{sin\dfrac{\left(k+1\right)x}{2}}{sin\dfrac{x}{2}}.2cos\dfrac{\left(k+1\right)x}{2}sim\dfrac{x}{2}\)\(=2sin\dfrac{\left(k+1\right)x}{2}cos\dfrac{\left(k+1\right)x}{2}=2sin\left(k+1\right)x\).
Vì vậy \(S_{k+1}=S_k+sin\left(k+1\right)x\).
Vậy điều cần chứng minh đúng với mọi n.

Lời giải:
Xét csn $(u_n)$ với công bội $q$
Ta có:
$S_n=u_1+u_2+...+u_n=u_1+u_1q+u_1q^2+....+u_1q^{n-1}$
$=u_1(1+q+q^2+....+q^{n-1})$
$qS_n=u_1(q+q^2+q^3+....+q^n)$
$\Rightarrow qS_n-S_n=u_1(q^n-1)$
$\Rightarrow S_n(q-1)=u_1(q^n-1)$
$\Rightarrow S_n=\frac{u_1(q^n-1)}{q-1}=\frac{u_1(1-q^n)}{1-q}$
Ta có đpcm.

\(u_3=u_2^2-u_2+2=4\)
\(S_1=1=\left(2-1\right)^2=\left(u_2-1\right)^2\)
\(S_2=2.5-1=9=\left(4-1\right)^2=\left(u_3-1\right)^2\)
Dự đoán \(S_n=\left(u_{n+1}-1\right)^2\)
Ta sẽ chứng minh bằng quy nạp:
- Với \(n=1;2\) đúng (đã kiểm chứng bên trên với \(S_1;S_2\))
- Giả sử đẳng thức đúng với \(n=k\)
Hay \(S_k=\left(u_1^2+1\right)\left(u_2^2+1\right)...\left(u_k^2+1\right)-1=\left(u_{k+1}-1\right)^2\)
Ta cần chứng minh:
\(S_{k+1}=\left(u_1^2+1\right)\left(u_2^2+1\right)...\left(u_k^2+1\right)\left(u_{k+1}^2+1\right)-1=\left(u_{k+2}-1\right)^2\)
Thật vậy:
\(S_{k+1}=\left[\left(u_{k+1}-1\right)^2+1\right]\left(u_{k+1}^2+1\right)-1\)
\(=\left(u_{k+1}^2-2u_{k+1}+2\right)\left(u_{k+1}^2+1\right)-1\)
\(=\left(u_{k+2}-u_{k+1}\right)\left(u_{k+2}+u_{k+1}-1\right)-1\)
\(=u_{k+2}^2-u_{k+2}-u_{k+1}^2+u_{k+1}-1\)
\(=u_{k+2}^2-u_{k+2}+2-u_{k+2}-1\)
\(=\left(u_{k+2}-1\right)^2\) (đpcm)

a) Năm số hạng đầu của dãy số là 3, √10, √11, √12, √13.
b) Ta có: u1 = 3 = √9 = √(1 + 8)
u2 = √10 = √(2 + 8)
u3 = √11 = √(3 + 8)
u4 = √12 = √(4 + 8)
...........
Từ trên ta dự đoán un = √(n + 8), với n ε N* (1)
Chứng minh công thức (1) bằng phương pháp quy nạp:
- Với n = 1, rõ ràng công thức (1) là đúng.
- Giả sử (1) đúng với n = k ≥ 1, tức là có uk = √(k + 8) với k ≥ 1.
Theo công thức dãy số, ta có:
uk+1 = .
Như vậy công thức (1) đúng với n = k + 1.

a) Năm số hạng đầu của dãy số là 3, √10, √11, √12, √13.
b) Ta có: u1 = 3 = √9 = √(1 + 8)
u2 = √10 = √(2 + 8)
u3 = √11 = √(3 + 8)
u4 = √12 = √(4 + 8)
...........
Từ trên ta dự đoán un = √(n + 8), với n ε N* (1)
Chứng minh công thức (1) bằng phương pháp quy nạp:
- Với n = 1, rõ ràng công thức (1) là đúng.
- Giả sử (1) đúng với n = k ≥ 1, tức là có uk = √(k + 8) với k ≥ 1.
Theo công thức dãy số, ta có:
uk+1 = .
Như vậy công thức (1) đúng với n = k + 1.

a) Năm số hạng đầu của dãy số là -1, 2, 5, 8, 11.
b) Chứng minh un = 3n - 4 bằng phương pháp quy nạp:
Với n =1 thì u1 3.1 - 4 = -1, đúng.
Giả sử hệ thức đúng với n = k ≥ 1, tức là uk = 3k -4. Ta chứng minh hệ thức cũng đúng với n = k + 1.
Thật vậy, theo công thức của dãy số và giả thiết quy nạp, ta có:
uk+1 = uk + 3 = 3k - 4 + 3 = 3(k + 1) - 4.
Vậy hệ thức đúng với mọi n ε N*
Lời giải:
Tổng của $n$ số hạng trong dãy là cấp số nhân $(u_n)$ với công bội $q$ là:
$S_n=u_1+u_2+....+u_n=u_1+u_1q+u_1q^2+...+u_1q^{n-1}$
$=u_1(1+q+q^2+....+q^{n-1})$
$qS_n=u_1(q+q^2+q^3+...+q^n)$
$\Rightarrow qS_n-S_n=u_1(q+q^2+q^3+...+q^n)-u_1(1+q+q^2+....+q^{n-1})$
$\Rightarrow S_n(q-1)=u_1(q^n-1)$
$\Rightarrow S_n=\frac{u_1(q^n-1)}{q-1}=\frac{u_1(1-q^n)}{1-q}$
Ta có đpcm.