
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

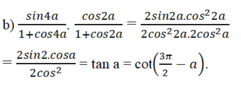

a: pi/2<a<pi
=>sin a>0
\(sina=\sqrt{1-\left(-\dfrac{1}{\sqrt{3}}\right)^2}=\dfrac{\sqrt{2}}{\sqrt{3}}\)
\(sin\left(a+\dfrac{pi}{6}\right)=sina\cdot cos\left(\dfrac{pi}{6}\right)+sin\left(\dfrac{pi}{6}\right)\cdot cosa\)
\(=\dfrac{\sqrt{3}}{2}\cdot\dfrac{\sqrt{2}}{\sqrt{3}}+\dfrac{1}{2}\cdot-\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{6}-2}{2\sqrt{3}}\)
b: \(cos\left(a+\dfrac{pi}{6}\right)=cosa\cdot cos\left(\dfrac{pi}{6}\right)-sina\cdot sin\left(\dfrac{pi}{6}\right)\)
\(=\dfrac{-1}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{2}-\dfrac{\sqrt{2}}{\sqrt{3}}\cdot\dfrac{1}{2}=\dfrac{-\sqrt{3}-\sqrt{2}}{2\sqrt{3}}\)
c: \(sin\left(a-\dfrac{pi}{3}\right)\)
\(=sina\cdot cos\left(\dfrac{pi}{3}\right)-cosa\cdot sin\left(\dfrac{pi}{3}\right)\)
\(=\dfrac{\sqrt{2}}{\sqrt{3}}\cdot\dfrac{1}{2}+\dfrac{1}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{2}=\dfrac{\sqrt{2}+\sqrt{3}}{2\sqrt{3}}\)
d: \(cos\left(a-\dfrac{pi}{6}\right)\)
\(=cosa\cdot cos\left(\dfrac{pi}{6}\right)+sina\cdot sin\left(\dfrac{pi}{6}\right)\)
\(=\dfrac{-1}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{2}+\dfrac{\sqrt{2}}{\sqrt{3}}\cdot\dfrac{1}{2}=\dfrac{-\sqrt{3}+\sqrt{2}}{2\sqrt{3}}\)

a: VT=sin^2a(sin^2a+cos^2a)+cos^2a
=sin^2a+cos^2a
=1=VP
b: \(VT=\dfrac{sina+sina\cdot cosa+sina-sina\cdot cosa}{1-cos^2a}=\dfrac{2sina}{sin^2a}=\dfrac{2}{sina}=VP\)
c: \(VT=\dfrac{sin^2a+1+2cosa+cos^2a}{sina\left(1+cosa\right)}\)
\(=\dfrac{2\left(cosa+1\right)}{sina\left(1+cosa\right)}=\dfrac{2}{sina}=VP\)

\(A=cos\left(\alpha+\dfrac{\pi}{6}\right)cos\left(\alpha-\dfrac{\pi}{6}\right)=\dfrac{1}{2}\left[cos\left(\alpha+\dfrac{\pi}{6}+\alpha-\dfrac{\pi}{6}\right)+cos\left(\alpha+\dfrac{\pi}{6}-\alpha+\dfrac{\pi}{6}\right)\right]\)
\(=\dfrac{1}{2}\left(cos2\alpha+cos\dfrac{\pi}{3}\right)=\dfrac{1}{2}\left(\dfrac{1}{4}+\dfrac{1}{2}\right)=\dfrac{3}{8}\)

1.a) \(4cos\dfrac{\alpha}{2}.cos\dfrac{\beta}{2}.cos\dfrac{f}{2}\)
\(=\dfrac{1}{2}.4\left[cos\left(\dfrac{\alpha-\beta}{2}\right)+cos\left(\dfrac{\alpha+\beta}{2}\right)\right].cos\dfrac{f}{2}\)
\(=2.cos\left(\dfrac{\alpha-\beta}{2}\right)cos\dfrac{f}{2}+2.cos\left(\dfrac{\alpha+\beta}{2}\right).cos\dfrac{f}{2}\)
\(=cos\left(\dfrac{\alpha-\left(\beta+f\right)}{2}\right)+cos\left(\dfrac{\alpha-\beta+f}{2}\right)+cos\left(\dfrac{\alpha+\beta-f}{2}\right)+cos\left(\dfrac{\alpha+\beta+f}{2}\right)\)
\(=cos\left(\dfrac{2\alpha-\pi}{2}\right)+cos\left(\dfrac{\pi-2\beta}{2}\right)+cos\left(\dfrac{\pi-2f}{2}\right)+cos\left(\dfrac{\pi}{2}\right)\)
\(=cos\left(-\dfrac{\pi}{2}+\alpha\right)+cos\left(\dfrac{\pi}{2}-\beta\right)+cos\left(\dfrac{\pi}{2}-f\right)\)
\(=sin\alpha+sin\beta+sinf\) (đpcm)
a2) \(1+4sin\dfrac{\alpha}{2}.sin\dfrac{\beta}{2}.sin\dfrac{f}{2}\)
\(=1+2\left[cos\left(\dfrac{\alpha-\beta}{2}\right)-cos\left(\dfrac{\alpha+\beta}{2}\right)\right].sin\dfrac{f}{2}\)
\(=1+2.cos\left(\dfrac{\alpha-\beta}{2}\right).sin\dfrac{f}{2}-2.cos\left(\dfrac{\alpha+\beta}{2}\right).sin\dfrac{f}{2}\)
\(=1+sin\left(\dfrac{f-\alpha+\beta}{2}\right)+sin\left(\dfrac{a-\beta+f}{2}\right)-sin\left(\dfrac{f-\left(\alpha+\beta\right)}{2}\right)-sin\left(\dfrac{\alpha+\beta+f}{2}\right)\)
\(=1+sin\left(\dfrac{\pi-2\alpha}{2}\right)+sin\left(\dfrac{\pi-2\beta}{2}\right)-sin\left(\dfrac{2f-\pi}{2}\right)-sin\left(\dfrac{\pi}{2}\right)\)
\(=sin\left(\dfrac{\pi}{2}-\alpha\right)+sin\left(\dfrac{\pi}{2}-\beta\right)+sin\left(\dfrac{\pi}{2}-f\right)\)
\(=cos\alpha+cos\beta+cosf\) (đpcm)

Đáp án D
Ta có
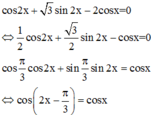
Do đó để phương trình ![]() tương đương với phương trình
tương đương với phương trình
![]()

Để giải bài toán này, ta sẽ sử dụng các công thức và quy tắc trong lượng giác để tính toán.
Trước hết, ta có: sin(α+β) = sinα.cosβ + cosα.sinβ cos(α+β) = cosα.cosβ - sinα.sinβ
Đề bài cho α+β = 1313 và tanα = -2tanβ. Ta có thể suy ra các thông tin sau: tanα = -2tanβ => sinα/cosα = -2sinβ/cosβ => sinα.cosβ = -2sinβ.cosα
Bài toán yêu cầu tính A = sin(α+3π/8) . cos(α+π/8) + sin(β-5π/12) . sin(β-π/12)
Để tính A, ta sẽ thay các giá trị đã biết vào công thức trên:
A = sin(α+3π/8) . cos(α+π/8) + sin(β-5π/12) . sin(β-π/12) = (sinα . cos(3π/8) + cosα . sin(3π/8)) . (cosα . cos(π/8) - sinα . sin(π/8)) + (sinβ . cos(5π/12) - cosβ . sin(5π/12)) . (cosβ . cos(π/12) + sinβ . sin(π/12)) = (sinα . cos(3π/8) + cosα . sin(3π/8)) . (cosα . cos(π/8) - sinα . sin(π/8)) + (sinβ . cos(5π/12) - cosβ . sin(5π/12)) . (cosβ . cos(π/12) + sinβ . sin(π/12)) = (sinα . cos(3π/8) + cosα . sin(3π/8)) . (cosα . cos(π/8) - sinα . sin(π/8)) + (sinβ . cos(5π/12) - cosβ . sin(5π/12)) . (cosβ . cos(π/12) + sinβ . sin(π/12)) = (sinα . cos(3π/8) + cosα . sin(3π/8)) . (cosα . cos(π/8) - sinα . sin(π/8)) + (sinβ . cos(5π/12) - cosβ . sin(5π/12)) . (cosβ . cos(π/12) + sinβ . sin(π/12))
Tuy nhiên, để tính giá trị chính xác của A, cần biết thêm giá trị cụ thể của α và β. Trong câu hỏi của bạn, không có thông tin về α và β, do đó không thể tính toán giá trị của A.

a) Do \(\begin{array}{l}\sin \alpha = MH \Rightarrow {\sin ^2}\alpha = M{H^2}\\\cos \alpha = OH \Rightarrow {\cos ^2}\alpha = O{H^2}\end{array}\)
Áp dụng định lý Py – Ta – Go vào tam giác OMH vuông tại H ta có:
\(\begin{array}{l}M{H^2} + O{H^2} = O{M^2} = 1\\ \Rightarrow {\sin ^2}\alpha + {\cos ^2}\alpha = 1\end{array}\)
b) Chia cả hai vế cho \({\cos ^2}\alpha \), ta được:
\(\begin{array}{l}\frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} + \frac{{{{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{1}{{{{\cos }^2}\alpha }}\\ \Leftrightarrow {\tan ^2}\alpha + 1 = \frac{1}{{{{\cos }^2}\alpha }}\end{array}\)
c) Chia cả hai vế cho \({\sin ^2}\alpha \), ta được:
\(\begin{array}{l}\frac{{{{\sin }^2}\alpha }}{{{{\sin }^2}\alpha }} + \frac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{1}{{{{\sin }^2}\alpha }}\\ \Leftrightarrow {\cot ^2}\alpha + 1 = \frac{1}{{{{\sin }^2}\alpha }}\end{array}\)