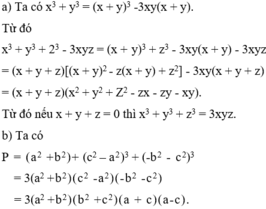Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,VT=\left(a^2+b^2\right)\left(c^2+d^2\right)=a^2c^2+b^2c^2+a^2d^2+b^2d^2\)
\(VP=\left(ac+bd\right)^2+\left(ad-bc\right)^2=a^2c^2+2abcd+b^2d^2+a^2d^2-2abcd+b^2c^2=a^2c^2+b^2c^2+a^2d^2+b^2d^2\)
\(\Rightarrow VT=a^2c^2+b^2c^2+a^2d^2+b^2d^2=VP\left(đpcm\right)\)
b, Tham khảo:Chứng minh hằng đẳng thức:(a+b+c)3= a3 + b3 + c3 + 3(a+b)(b+c)(c+a) - Hoc24

Vì a,b,c là 3 cạnh tam giác nên \(a+b>c\Leftrightarrow ac+bc>c^2\)
CMTT: \(ab+bc>b^2;ab+ac>a^2\)
Cộng vế theo vế \(\Leftrightarrow a^2+b^2+c^2< ab+bc+ca+ab+bc+ca\)
\(\Leftrightarrow a^2+b^2+c^2< 2ab+2bc+2ca\\ \Leftrightarrow a^2+b^2+c^2-2ab-2bc-2ca< 0\)

BĐT cần chứng minh tương đương:
\(a^2+b^2+c^2\ge2ab-2bc+2ca\)
\(\Leftrightarrow a^2+b^2+c^2+2bc-2a\left(b+c\right)\ge0\)
\(\Leftrightarrow a^2+\left(b+c\right)^2-2a\left(b+c\right)\ge0\)
\(\Leftrightarrow\left(a-b-c\right)^2\ge0\) (luôn đúng)
Vậy BĐT đã cho đúng

Ta có:\(x+y=a\)
=>\(x^2+2xy+y^2=a^2\)
=>\(x^2+y^2=a^2-2xy=a^2-2b\left(đpcm\right)\)
Ta lại có:\(x^3+3x^2y+3xy^2+y^3=a^3\)
=>\(x^3+y^3+3xy\left(x+y\right)=a^3\)
=>\(x^3+y^3=a^3-3xy\left(x+y\right)=a^3-3ab\left(đpcm\right)\)
b)\(a+b+c=0\) =>\(a^3+b^3+c^3+3a^2b+3ab^2+3b^2c+3bc^2+3c^2a+3a^2c+6abc=0\) =>\(a^3+b^3+c^3+3\left(a+b\right)\left(a+c\right)\left(b+c\right)=0\) =>\(a^3+b^3+c^3+3\left(-a\right)\left(-b\right)\left(-c\right)=0\) =>\(a^3+b^3+c^3=3abc\left(đpcm\right)\)

a) \(\left(a+b+c\right)^2+a^2+b^2+c^2\)
\(=a^2+b^2+c^2+2ab+2bc+2ca+a^2+b^2+c^2\)
\(=a^2+2ab+b^2+b^2+2bc+c^2+c^2+2ca+a^2\)
\(=\left(a+b\right)^2+\left(b+c\right)^2+\left(c+a\right)^2\)
b) \(\left(a+b+c\right)^3-a^3-b^3-c^3\)
\(=\left(b+c\right)\left[\left(a+b+c\right)^2+\left(a+b+c\right)a+a^2\right]-\left(b+c\right)\left(b^2+bc+c^2\right)\)
\(=\left(b+c\right)\left(3a^2+3ab+3bc+3ac\right)\)
\(=3\left(a+b\right)\left(b+c\right)\left(c+a\right)\)