K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
VT
2
22 tháng 12 2016
\(\left(2x+3\right)^2=25\)
\(\Rightarrow2x+3=5\) hoặc \(2x+3=-5\)
+) \(2x+3=5\Rightarrow2x=2\Rightarrow x=1\)
+) \(2x+3=-5\Rightarrow2x=-8\Rightarrow x=-4\)
Vậy \(x\in\left\{1;-4\right\}\)
22 tháng 12 2016
\(\left(2x+3\right)^2=25\)
\(\Rightarrow\left(2x+3\right)^2=5^2=\left(-5\right)^2\)
\(\Rightarrow2x+3=\pm5\)
* Với \(2x+3=5\)
\(2x=5-3\)
\(2x=2\)
\(x=2\div2\)
\(x=1\)
* Với \(2x+3=-5\)
\(2x=-5-3\)
\(2x=-8\)
\(x=-8\div2\)
\(x=-4\)
Vậy \(x\in\left\{1;-4\right\}\)
D
2
14 tháng 12 2021
GIÚP MIK VS NHA:(((((
CẢM ƠN RẤT NHIỀU
MN XONG CÂU NÀO THÌ CỨ GỬI LUÔN CHO MIK CÂU ĐÓ NHA;-;
MIK CÒN CHÉP KỊP
:(((((((((((((( NHANHH NHANH GIÚP MIK Ạ
14 tháng 12 2021
Câu 1:
\(a,\dfrac{x}{4}=\dfrac{y}{7}=\dfrac{x-y}{4-7}=\dfrac{-15}{-3}=5\\ \Rightarrow\left\{{}\begin{matrix}x=20\\y=35\end{matrix}\right.\\ b,\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{x+y}{3+5}=\dfrac{-32}{8}=-4\\ \Rightarrow\left\{{}\begin{matrix}x=-12\\y=-20\end{matrix}\right.\\ c,\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{5}=\dfrac{x+y+z}{2+3+5}=\dfrac{-90}{10}=-9\\ \Rightarrow\left\{{}\begin{matrix}x=-18\\y=-27\\z=-45\end{matrix}\right.\\ d,\dfrac{x}{4}=\dfrac{y}{2}=\dfrac{z}{7}=\dfrac{2x-4y+3z}{8-8+21}=\dfrac{42}{21}=2\\ \Rightarrow\left\{{}\begin{matrix}x=8\\y=4\\z=14\end{matrix}\right.\)
\(e,\dfrac{x}{5}=\dfrac{y}{6}=\dfrac{z}{7}=\dfrac{z-x}{7-5}=\dfrac{30}{2}=15\\ \Rightarrow\left\{{}\begin{matrix}x=75\\y=90\\z=105\end{matrix}\right.\\ f,\Rightarrow\dfrac{x}{3}=\dfrac{y}{5};\dfrac{x}{4}=\dfrac{z}{3}\Rightarrow\dfrac{x}{12}=\dfrac{y}{20}=\dfrac{z}{9}=\dfrac{x-y-z}{12-20-9}=\dfrac{-68}{-17}=4\\ \Rightarrow\left\{{}\begin{matrix}x=48\\y=80\\z=36\end{matrix}\right.\\ g,\Rightarrow\dfrac{x}{6}=\dfrac{y}{4}=\dfrac{z}{3}=\dfrac{x+y+z}{6+4+3}=\dfrac{65}{13}=5\\ \Rightarrow\left\{{}\begin{matrix}x=30\\y=20\\z=15\end{matrix}\right.\\ h,\Rightarrow\dfrac{x}{4}=\dfrac{y}{6};\dfrac{y}{5}=\dfrac{z}{8}\Rightarrow\dfrac{x}{20}=\dfrac{y}{30}=\dfrac{z}{48}=\dfrac{5x-3y-3z}{100-90-144}=\dfrac{-536}{-134}=4\\ \Rightarrow\left\{{}\begin{matrix}x=80\\y=120\\z=192\end{matrix}\right.\)
NT
2
TM
9 tháng 6 2017
ta có P(x)=x^2+ax+b ; Q(x)=x^2+cx+d
ta có x1 và x2 là nghiêm của P(x)Dán
nên \(x_1^2+ax_1+b=0;x_2^2+ax_2+b=0\)
\(\Rightarrow x_1^2=-ax_1-b\) và \(x_2^2=-ax_2-b\) (1)
Ta có x1,x2 là nghiêm của Q(x)
nên \(x_1^2+cx_1+d=0;x_2^2+cx_2+d=0\)
\(\Rightarrow x_1^2=-cx_1-d\)và \(x_2^2=-cx_2-d\) (2)
Từ (1) và (2) suy ra \(-ax_1-b=-cx_1-d\\ -ax_2-b=-cx_2-d\)
Do đó \(ax_1+b=cx_1+d\\ ax_2+b=+cx_2+d\)
Suy ra\(x_1^2+ax_1+b=x^2_1+cx_1+d\\ x^2_2+ax_2+b=x^2_2+cx_2+d\)
Nên P(x)=Q(x)
NM
10 tháng 6 2017
Q(x) =x2 +ax + b
P(x) = x2 +cx + d
Vì x1;x2 đều là nghiệm của P(x); Q(x)
=>x1;x2 là nghiệm của : P(x) - Q(x)=(c-a)x +(d-b)
=> PT: (c-a)x +(d-b) =0 có 2 nghiệm x1;x2
=>\(\left\{{}\begin{matrix}c-a=0\\d-b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=c\\b=d\end{matrix}\right.\)
Nên => P(x) = Q(x) dpcm
30 tháng 12 2021
\(\text{f(1)=}2.1^2+1=3\)
\(\text{f(-1)=}2.\left(-1\right)^2+1=3\)
\(\text{f(2)=}2.2^2+1=9\)
\(\text{f(0)=}2.0^2+1=1\)
\(\text{f(-3)=}=2.\left(-3\right)^2+1=19\)
25 tháng 12 2021
a: Xét ΔBID và ΔBIC có
BI chung
\(\widehat{BID}=\widehat{BIC}\)
BD=BC
Do đó: ΔBID=ΔBIC
20 tháng 8 2023
\(=\dfrac{3\left(\dfrac{1}{1}+\dfrac{1}{3}+\dfrac{1}{5}+...+\dfrac{1}{99}\right)}{\dfrac{1}{100}\left(\dfrac{100}{1\cdot99}+\dfrac{100}{3\cdot97}+...+\dfrac{100}{99\cdot1}\right)}\)
\(=\dfrac{3\left(1+\dfrac{1}{3}+\dfrac{1}{5}+...+\dfrac{1}{99}\right)}{\dfrac{1}{100}\cdot\left(\dfrac{1}{1}+\dfrac{1}{99}+\dfrac{1}{3}+\dfrac{1}{97}+...+\dfrac{1}{99}+\dfrac{1}{1}\right)}\)
\(=\dfrac{3\left(1+\dfrac{1}{3}+\dfrac{1}{5}+...+\dfrac{1}{99}\right)}{\dfrac{1}{50}\left(1+\dfrac{1}{3}+\dfrac{1}{5}+...+\dfrac{1}{99}\right)}=3:\dfrac{1}{50}=150\)
17 tháng 10 2021
Bài 3:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{2}=\dfrac{b}{5}=\dfrac{a+b}{2+5}=\dfrac{70}{7}=10\)
Do đó: a=20; b=50
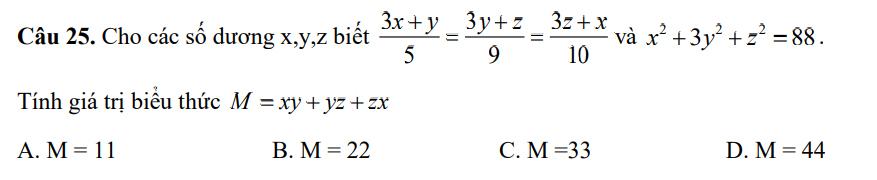
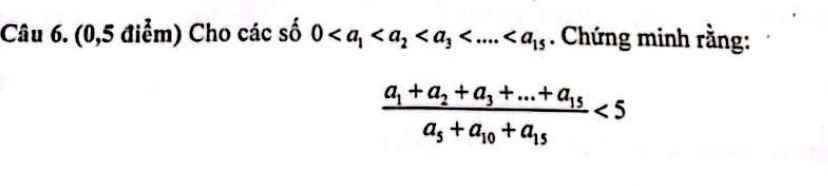
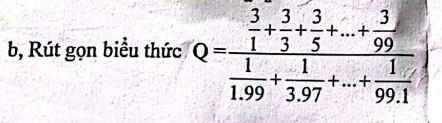
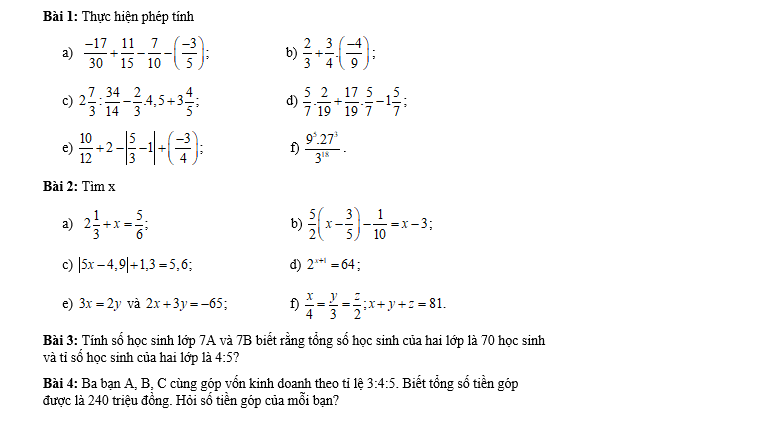
\(\widehat{A}=180^o-\widehat{B}-\widehat{C}=180^o-40^o-40^o=100^o\)
=> \(\widehat{A_{ngoai}}=180^o-100^o=80^o\)
=> \(\widehat{DAB}=\dfrac{1}{2}\widehat{A_{ngoai}}=\dfrac{1}{2}\cdot80^o=40^o\)
Ta có: \(\widehat{DAB}=\widehat{ABC}\left(=40^o\right)\)
Mà 2 góc này ở vị trí so le trong
=> AD//BC
cậu giúp mik nhiều ghê, cám ơn nha