
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Thực hiện phép nhân đa thức với đa thức ở vế trái.
=> VT = VP (đpcm)

\(\left(a+b+c\right)^2=a^2+b^2+c^2\)
=>\(a^2+b^2+c^2+2\left(ab+bc+ac\right)=a^2+b^2+c^2\)
=>\(2\left(ab+bc+ac\right)=0\)
=>ab+bc+ac=0
\(\dfrac{1}{a^3}+\dfrac{1}{b^3}+\dfrac{1}{c^3}=\dfrac{3}{abc}\)
=>\(\dfrac{\left(bc\right)^3+\left(ac\right)^3+\left(ab\right)^3}{\left(abc\right)^3}=\dfrac{3}{abc}\)
=>\(\left(bc\right)^3+\left(ac\right)^3+\left(ab\right)^3=3\left(abc\right)^2\)
\(\Leftrightarrow\left(ab+bc\right)^3-3\cdot ab\cdot bc\cdot\left(ab+bc\right)+\left(ac\right)^3=3\left(abc\right)^2\)
=>\(\left(-ac\right)^3-3\cdot ab\cdot bc\cdot\left(-ac\right)+\left(ac\right)^3-3\left(abc\right)^2=0\)
=>\(-a^3c^3+a^3c^3+3a^2b^2c^2-3a^2b^2c^2=0\)
=>0=0(đúng)

Do a;b;c là 3 cạnh của 1 tam giác
\(\Rightarrow a< b+c\Rightarrow2a< a+b+c=6\Rightarrow a< 3\)
Chứng minh tương tự ta được: \(b< 3;c< 3\)
\(\Rightarrow3-a>0;3-b>0,3-c>0\)
Do đó:
\(\left(3-a\right)\left(3-b\right)\left(3-c\right)\le\left(\dfrac{3-a+3-b+3-c}{3}\right)^3=\left(\dfrac{9-\left(a+b+c\right)}{3}\right)^3=1\)
\(\Leftrightarrow-abc+3\left(ab+bc+ca\right)-9\left(a+b+c\right)+27\le1\)
\(\Leftrightarrow-abc+3\left(ab+bc+ca\right)-27\le1\)
\(\Leftrightarrow abc\ge3\left(ab+bc+ca\right)-28\)
\(\Leftrightarrow2abc\ge6\left(ab+bc+ca\right)-56\)
\(\Leftrightarrow3\left(a^2+b^2+c^2\right)+2abc\ge3\left(a^2+b^2+c^2\right)+6\left(ab+bc+ca\right)-56\)
\(\Leftrightarrow3\left(a^2+b^2+c^2\right)+2abc\ge3\left(a+b+c\right)^2-56=52\) (đpcm)
Dấu "=" xảy ra khi \(a=b=c=2\)
BĐT vế phải:
Vẫn từ chứng minh trên, \(3-a>0;3-b>0,3-c>0\)
\(\Rightarrow\left(3-a\right)\left(3-b\right)\left(3-c\right)>0\)
\(\Leftrightarrow-abc+3\left(ab+bc+ca\right)-9\left(a+b+c\right)+27>0\)
\(\Leftrightarrow-abc+3\left(ab+bc+ca\right)-27>0\)
\(\Leftrightarrow abc< 3\left(ab+bc+ca\right)-27\)
\(\Leftrightarrow2abc< 6\left(ab+bc+ca\right)-54\)
\(\Leftrightarrow3\left(a^2+b^2+c^2\right)+2abc< 3\left(a^2+b^2+c^2\right)+6\left(ab+bc+ca\right)-54\)
\(\Leftrightarrow3\left(a^2+b^2+c^2\right)+2abc< 3\left(a+b+c\right)^2-54=54\) (đpcm)

a. -Xét △AID: AD//BJ (ABCD là hình bình hành).
\(\Rightarrow\dfrac{IA}{IJ}=\dfrac{ID}{IB}\) (định lí Ta-let). (1)
-Xét △AIB: AB//DK (ABCD là hình bình hành).
\(\Rightarrow\dfrac{IK}{IA}=\dfrac{ID}{IB}\) (định lí Ta-let). (2)
-Từ (1), (2) suy ra: \(\dfrac{IA}{IJ}=\dfrac{IK}{IA}\) nên \(IA^2=IK.IJ\).
b. -Có: \(\dfrac{IA}{IJ}=\dfrac{IK}{IA}\) (cmt)
\(\Rightarrow\dfrac{IA+IJ}{IJ}=\dfrac{IK+IA}{IA}\)
\(\Rightarrow\dfrac{AJ}{IJ}=\dfrac{AK}{IA}\)
\(\Rightarrow\dfrac{AK}{IA}=\dfrac{AJ+AK}{IJ+IA}=\dfrac{AJ+AK}{AJ}\)
\(\Rightarrow\dfrac{1}{IA}=\dfrac{AJ+AK}{AJ.AK}\)
\(\Rightarrow\dfrac{1}{IA}=\dfrac{1}{AK}+\dfrac{1}{AJ}\)


Vì \(a^2+b^2\ge2ab,b^2+1\ge2b\),ta có:
\(\frac{1}{a^2+2b^2+3}=\frac{1}{a^2+b^2+b^2+1+1}\le\frac{1}{2\left(ab+b+1\right)}\)
Tương tự:\(\frac{1}{b^2+2c^2+3}\le\frac{1}{2\left(bc+c+1\right)}\)và \(\frac{1}{b^2+2c^2+3}\le\frac{1}{2\left(bc+c+1\right)}\)
Khi đó\(A\le\frac{1}{2}\left(\frac{1}{ab+b+1}+\frac{1}{bc+c+1}+\frac{1}{ca+a+a}\right)\)
\(\Leftrightarrow A\le\frac{1}{2}\left(\frac{1}{ab+b+1}+\frac{ab}{ab+b+1}+\frac{b}{ab+b+1}\right)=\frac{1}{2}\)
Dấu"="trg BĐT trên xảy ra khi \(a=b=c=1\)
Vậy \(Max_P=\frac{1}{2}\Leftrightarrow a=b=c=1\)
Chắc không được GP đâu !!
Áp dụng bđt cauchy , ta có :
+) \(a^2+2b^2+3=\left(a^2+b^2\right)+\left(b^2+1\right)+2\ge2ab+2b+2\)
+) \(b^2+2c^2+3\ge2bc+2c+2\)
+) \(c^2+2a^2+3\ge2ac+2a+2\)
Khi đó , ta có :
\(VT\le\frac{1}{2ab+2b+2}+\frac{1}{2bc+2c+2}+\frac{1}{2ac+2a+2}\)
\(=\frac{1}{2}\left(\frac{1}{ab+b+1}+\frac{1}{bc+c+1}+\frac{1}{ac+a+1}\right)\)
\(=\frac{1}{2}\left(\frac{1}{ab+b+1}+\frac{abc}{bc+c+1}+\frac{abc}{ac+a+1}\right)\)( vì abc= 1 )
\(=\frac{1}{2}=VP\)( đoạn này ban tự phân tích ra nha , mk lmaf hơi tắt )
Vậy .................
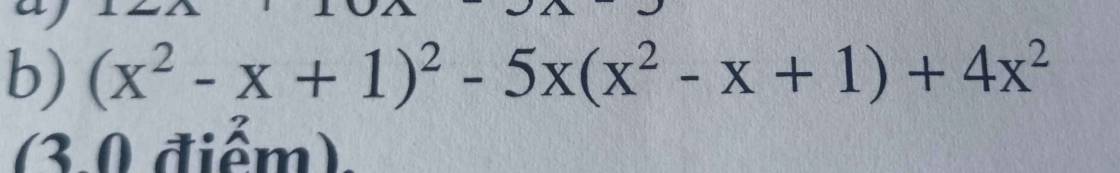
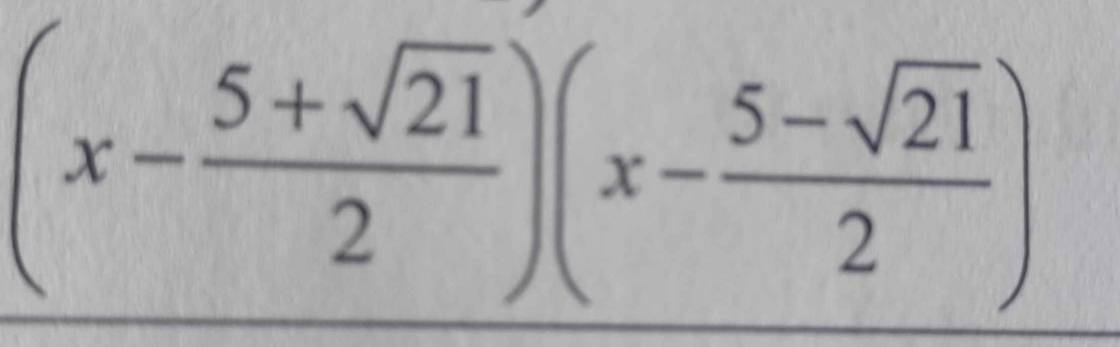
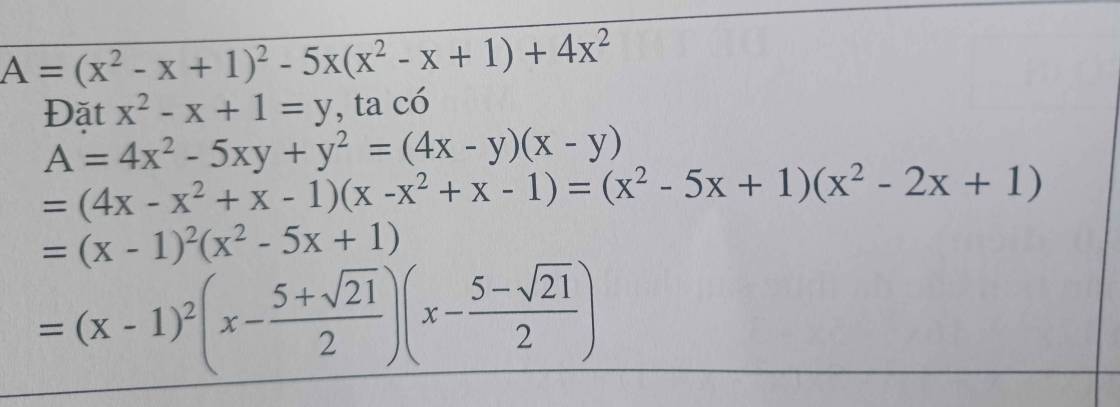
Đề bài sai
Phản ví dụ: \(a=c=0;b=-2\) thì \(a^4+b^3+c^2+1=-7\)
Trong khi \(a\left(ab^2-a+c+1\right)=0\)
\(-7\) ko thể lớn hơn 0