MD
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CW
13 tháng 5 2016
Câu 1:
Xét tam giác ABD và tam giác ACD:
ADB= ADC =90o
AD chung
DB= DC
=> tam giác ABD = tam giác ACD (2 cạnh góc vuông)
=> góc B = góc C (2 góc tương ứng)
Vậy tam giác ABC cân
Câu 2:
Chứng minh y chang câu 1
Câu 3:
Xét tam giác ABD và tam giác ACD:
ADB= ADC =90o
AD chung
BAD = CAD
=> tam giác ABD = tam giác ACD (cạnh góc vuông_ góc nhọn)
=> góc B = góc C (2 góc tương ứng)
Vậy tam giác ABC cân
Câu 4:
Chứng minh giống hệt câu 3.
TT
chứng minh rằng trong một tam giác có 1 đg trung tuyến đồng thời là đg phân giác thì tam giác đó cân
0
TT
1
24 tháng 3 2016
giả sử đó là tam giác abc, am là trugn tuyến của tam giác abc =>mb=mc
vì am là đg phân giác => góc mab = góc mac
Xét tam giác amb và tam giác amc có:
góc mab = góc mac(cmt)
mb=mc (cmt)
am chung
=> tam giác amb= tam giác amc(c.g.c)
=> <mab=<mac( hia cạnh tg ứng)
xét tam giác abc có <b=<c (chứng minh trên)
= tam giác abc cân
CM
2 tháng 6 2019
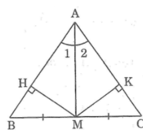
Kẻ MH ⊥ AB, MK ⊥ AC
Vì AM là tia phân giác của ∠(BAC) nên MH = MK (tính chất tia phân giác)
Xét hai tam giác MHB và MKC, ta có:
∠(MHB) = ∠(MKC) = 90º
MH = MK (chứng minh trên)
MB = MC (gt)
Suy ra: ΔMHB = ΔMKC (cạnh huyền, cạnh góc vuông)
Suy ra: ∠B = ∠C (hai góc tương ứng)
Vậy tam giác ABC cân tại A.
CM
10 tháng 4 2018
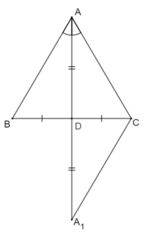
- Giả sử AD vừa là đường trung tuyến, vừa là đường phân giác của tam giác ABC.
Ta cần chứng minh ∆ABC cân tại A.
Kéo dài AD một đoạn DA1 sao cho DA1 = AD.
- ∆ADB và ∆A1DC có
AD = DA1 (cách vẽ)
BD = CD (do D là trung điểm BC)
⇒ ∆ADB = ∆A1DC (c.g.c)
⇒ 
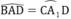(hai góc tương ứng), AB = A1C (hai cạnh tương ứng) (1)
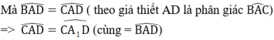
⇒ ∆ACA1 cân tại C ⇒ AC = A1C (2)
Từ (1) và (2) ⇒ AB = AC.
Vậy ∆ABC cân tại A
Tức là: Nếu tam giác có một đường trung tuyến đồng thời là đường phân giác thì tam giác đó là một tam giác cân.
DV
17 tháng 5 2017
Khi một tam giác có đường trung tuyến đồng thời là đường phân giác thì đó là tam giác cân.
Ở đây tam giác ABC có AM là trung tuyến đồng thời là phân giác vậy
=> tam giác ABC là tam giác cân (tính chất tam giác cân)
25 tháng 5 2017
Ta có hình vẽ :
Trên tia đổi của tia MA lấy điểm H sao cho MA=MH
Xét \(\Delta MBH\) và \(\Delta MCA\) có:
\(\left\{{}\begin{matrix}AM=HM\left(theocachve\right)\\\widehat{BMH}=\widehat{CMA\left(\text{đ}^2\right)}\\BM=CM\left(AMlatrungtuyen\right)\end{matrix}\right.\)
=> \(\Delta MBH\) = \(\Delta MCA\) (c.g.c)
=> +) BH=CA ( hai cạnh tương ứng) (1)
+) \(\widehat{BHM}=\widehat{CAM}\) ( hai góc tương ứng ) (2)
Ta lại có:
AM là phân giác => \(\widehat{BAM}=\widehat{MAC}\) (3)
Từ (2) và (3) suy ra: \(\widehat{BAM}=\widehat{MHB}\)
=> \(\Delta HBA\) là tam giác cân ( vì có hai góc ở đáy bằng nhau )
=> AB=HB ( hai cạnh bên của tam giác cân ) (4)
Từ (1) và (4) suy ra :
AB=AC
=> \(\Delta ABC\) là tam giác cân ( vì có hai cạnh trong tam giác bằng nhau )
( đ.p.c.m )
bn vẽ tam giác cân ABC, vẽ AM là trung tuyến vừa là p/giác của tam giác
giải: kẻ MH vuông góc AB ; MK vuông góc AC
vì AM là trung tuyến vừa là p/giác của góc BAC
=> MH = MK
xét 2 tam giác vuông HBM và tam giác KCM có:
MH = MK (cmt)
BM = CM (gt)
=> tam giác HBM = tam giác KCM (ch-cgv)
=> góc B = góc C (góc tương ứng)
=> tam giác ABC cân tại A