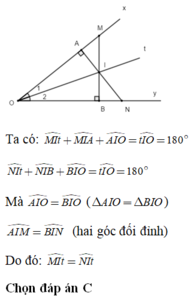
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

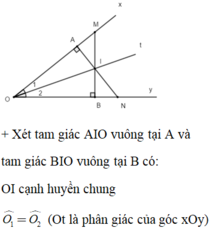
Do đó: Δ A I O = Δ B I O (cạnh huyền – góc nhọn)
Suy ra OA = OB ; IA = IB (hai cạnh tương ứng)
+ Xét tam giác IAM vuông tại A và tam giác IBN vuông tại B có:
IA = IB (cmt)


Xét \(\Delta AOD\)và \(\Delta COB\)
\(OA=OC\left(gt\right)\)
\(AOD=COB\left(=90-DOC\right)\)
\(OD=OB\left(gt\right)\)
\(\Rightarrow\Delta AOD=\Delta COB\left(c.g.c\right)\Rightarrow ADO=CBO\left(1\right)\)
Gọi giao điểm của BF và OD là M
\(\)Ta có \(FMD=OMB\left(2\right)\)(đối đỉnh)
\(\left(1\right)\left(2\right)\Rightarrow ADO+FMD=OMB+CBO\Rightarrow FDM+FMD=MBO+OMB\)
\(\Rightarrow180-MFD=180-MOB=180-90\left(MOB=DOB=90\right)\Rightarrow MFD=90\)
Vậy \(BF\perp AD\)
Gọi E là giao điểm của Oy và AD
Ta có: \(\widehat{O_1}+\widehat{O_2}=\widehat{COB}\)(do tia OA nằm giữa hai tia OC và OB)
\(\widehat{O_3}+\widehat{O_2}=\widehat{AOD}\)(do tia OB nằm giữa hai tia OA và OD)
Mà \(\widehat{O_1}=\widehat{O_3}=90^o\)(do \(Oz\perp Ox,Ot\perp Oy\))
Do đó: \(\widehat{COB}=\widehat{AOD}\)
\(\Delta AOD\)và \(\Delta COB\)có:
\(\widehat{COB}=\widehat{AOD}\)(c.m.t)
OA = OC (theo gt)
OB = OD (theo gt)
Do đó: \(\Delta AOD\)=\(\Delta COB\)(c.g.c)
\(\Delta FBE\) có: \(\widehat{EFB}+\widehat{FEB}+\widehat{FBE}=180^o\)(theo định lí tổng ba góc của một tam giác)
\(\Delta OED\) có: \(\widehat{O_3}+\widehat{ODE}+\widehat{OED}=180^o\)(theo định lí tổng ba góc của một tam giác)
Mà \(\widehat{FBE}=\widehat{ODE}\) (do \(\Delta COB\)= \(\Delta AOD\))
\(\widehat{FEB}=\widehat{OED}\)(2 góc đối đỉnh)
Suy ra: \(\widehat{EFB}=\widehat{O_3}\)
Mà \(\widehat{O_3}=90^o\)(do \(Oy\perp Ot\))
Do đó: \(\widehat{EFB}=90^o\)nên \(BF\perp FA\)
mik nha, mik mất công làm lắm đó! ^_^

a: Xét ΔOIA vuông tại A và ΔOIB vuông tại B có
OI chung
\(\widehat{AOI}=\widehat{BOI}\)
Do đó: ΔOIA=ΔOIB
b: Xét ΔOAD vuông tại A và ΔOBC vuông tại B có
OA=OB
\(\widehat{BOC}\) chung
Do đó: ΔOAD=ΔOBC
Suy ra: OD=OC
Xét ΔOIC và ΔOID có
OC=OD
\(\widehat{COI}=\widehat{DOI}\)
OI chung
Do đó: ΔOIC=ΔOID
c: Ta có: ΔOCD cân tại O
mà OI là đường phân giác
nên OI là đường cao

P/s: sửa I là điểm chứ không phải là trung điểm
Hình tự vẽ :<
a) Xét \(\Delta\)AOI và \(\Delta\)BOI có:
IAO=IBO (=90o)
IO: chung
AOI=BOI (OI: p/g AOB)
\(\Rightarrow\Delta\)AOI=\(\Delta\)BOI (ch-gn)
\(\Rightarrow\)IA=IB (2 cạnh tương ứng)
b) Xét \(\Delta\)KOB và \(\Delta\)MOA có:
KBO=MAO (\(\Delta\)AOI=\(\Delta\)BOI)
OB=OA ( \(\Delta\)AOI=\(\Delta\)BOI)
O: chung
\(\Rightarrow\)\(\Delta\)KOB=\(\Delta\)MOA (g.c.g)
\(\Rightarrow\)OK=OM (2 cạnh tương ứng)
Ta có:
\(\hept{\begin{cases}OA+AK=OK\\OB+BM=OM\end{cases}}\)mà \(\hept{\begin{cases}OA=OB\\OK=OM\end{cases}}\)
\(\Rightarrow\)AK=BM
c) Ta có: OM=OK (cmt)
\(\Rightarrow\)\(\Delta\)KOM cân tại O
\(\Rightarrow\)OMK=OKM
Xét \(\Delta\)OCM và \(\Delta\)OCK có:
OMK=OKM (cmy)
OC: chung
COM=COK (OC: p/g MOK)
\(\Rightarrow\)\(\Delta\)OCM=\(\Delta\)OCK (g.c.g)
\(\Rightarrow\)OCM=OCK (2 góc tương ứng)
Mà OCM+OCK=180o (kề bù)
\(\Rightarrow\)OCM=OCK=180o:2=90o
\(\Rightarrow\)OC \(\perp\) MK

a: Xét ΔOIA vuông tại A và ΔOIB vuông tại B có
OI chung
\(\widehat{AOI}=\widehat{BOI}\)
Do đó: ΔOIA=ΔOIB
b: Xét ΔOBC vuông tại B và ΔOAD vuông tại A có
OB=OA
\(\widehat{BOC}\) chung
Do đó: ΔOBC=ΔOAD
Suy ra: OC=OD
Xét ΔOIC và ΔOID có
OI chung
\(\widehat{COI}=\widehat{DOI}\)
OC=OD
Do đó: ΔOIC=ΔOID
c: Ta có: ΔOCD cân tại O
mà OI là đường phân giác
nên OI là đường cao

gt : \(\widehat{xOy}< 90^{\text{o}}\), \(\widehat{xOI}=\widehat{Ioy}\), \(IA\perp Ox\), \(IB\perp Oy\).
kl : .
c/m : Xét và , có :
\(OI\) là cạnh chung
\(\widehat{xOI}=\widehat{IOy}\left(gt\right)\)
\(\Rightarrow\) (ch - gn)
\(\Rightarrow IA=IB\) (2 cạnh tương ứng) (đpcm)
< Em tự vẽ hình nhé! >
+, Xét tam giác IAO và tam giác IBO có :
IO chung
Góc AOI = Góc IOB ( vì OI là tia phân giác của góc xOy)
Góc IAO = Góc IOB = 90 độ (gt)
=> Tam giác IAO = tam giác IBO ( ch-gn)
=> IA = IB ( 2 cạnh tương ứng )