Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt \(OA=OB=2OC=2a\)
\(\Rightarrow BC=\sqrt{OB^2+OC^2}=a\sqrt{5}\) \(\Rightarrow OM=\dfrac{1}{2}BC=\dfrac{a\sqrt{5}}{2}\)
Qua B kẻ đường thẳng song song OM cắt OC kéo dài tại D
\(\Rightarrow OM\) là đường trung bình tam giác BCD \(\Rightarrow BD=2OM=a\sqrt{5}\)
\(OM||BD\Rightarrow\left(OM;AB\right)=\left(BD;AB\right)=\widehat{ABD}\)
\(AB=\sqrt{OA^2+OB^2}=2a\sqrt{2}\)
\(AD=\sqrt{OA^2+OD^2}=\sqrt{OA^2+OC^2}=a\sqrt{5}\)
\(\Rightarrow cos\widehat{ABD}=\dfrac{AB^2+BD^2-AD^2}{2AB.BD}=\dfrac{\sqrt{10}}{5}\)

Cậu gán giá trị OA=OB=OC=1 và tình cho dễ nhé. Đặc biệt hóa ý

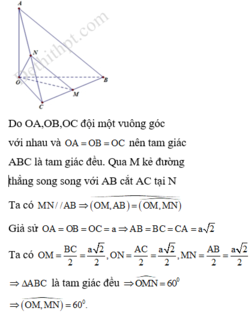
Gọi N là trung điểm AC \(\Rightarrow MN||AB\Rightarrow\widehat{OMN}\) là góc giữa OM và AB
Đặt \(OA=a\)
\(AB=\sqrt{OA^2+OB^2}=\sqrt{a^2+k^2a^2}=a\sqrt{k^2+1}\)
\(AC=\sqrt{OA^2+OC^2}=a\sqrt{k^2+1}\)
\(BC=\sqrt{OB^2+OC^2}=a.k\sqrt{2}\)
\(MN=\dfrac{1}{2}AB=\dfrac{a}{2}\sqrt{k^2+1}\) ; \(OM=\dfrac{BC}{2}=a.\dfrac{k\sqrt{2}}{2}\) ; \(ON=\dfrac{1}{2}AC=a.\dfrac{\sqrt{k^2+1}}{2}\)
\(cos\widehat{OMN}=cos60^0=\dfrac{OM^2+MN^2-ON^2}{2OM.MN}=\dfrac{1}{2}\)
\(\Leftrightarrow\dfrac{a^2.\dfrac{k^2}{2}}{2.a^2.\dfrac{k\sqrt{2k^2+2}}{4}}=\dfrac{1}{2}\Leftrightarrow2k=\sqrt{2k^2+2}\)
\(\Leftrightarrow4k^2=2k^2+2\Rightarrow k=1\)

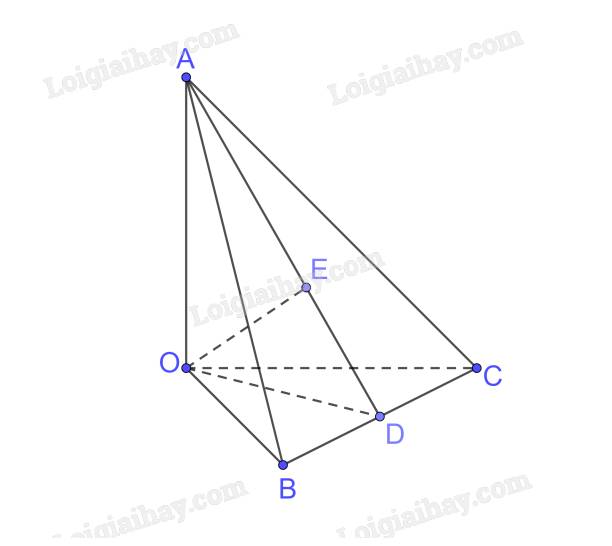
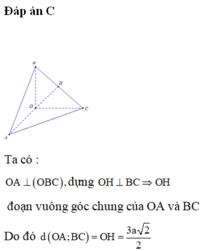
Ta có \(OA \bot OB,OA \bot OC \Rightarrow OA \bot \left( {OBC} \right);BC \subset \left( {OBC} \right) \Rightarrow OA \bot BC\)
Trong (OBC) kẻ \(OD \bot BC\)
\(\begin{array}{l} \Rightarrow BC \bot \left( {OAD} \right);BC \subset \left( {ABC} \right) \Rightarrow \left( {OAD} \right) \bot \left( {ABC} \right)\\\left( {OAD} \right) \cap \left( {ABC} \right) = AD\end{array}\)
Trong (OAD) kẻ \(OE \bot AD\)
\( \Rightarrow OE \bot \left( {ABC} \right) \Rightarrow d\left( {O,\left( {ABC} \right)} \right) = OE\)
Xét tam giác OBC vuông tại O có
\(\frac{1}{{O{D^2}}} = \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}} = \frac{1}{{{{\left( {a\sqrt 2 } \right)}^2}}} + \frac{1}{{{{\left( {2a} \right)}^2}}} = \frac{3}{{4{a^2}}} \Rightarrow OD = \frac{{2a\sqrt 3 }}{3}\)
Xét tam giác OAD vuông tại O có
\(\frac{1}{{O{E^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{D^2}}} = \frac{1}{{{a^2}}} + \frac{1}{{{{\left( {\frac{{2a\sqrt 3 }}{3}} \right)}^2}}} = \frac{7}{{4{a^2}}} \Rightarrow OE = \frac{{2a\sqrt 7 }}{7}\)
Vậy \(d\left( {O,\left( {ABC} \right)} \right) = \frac{{2a\sqrt 7 }}{7}\)