Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(15 \in \mathbb{N}\)
b) \(10,5 \notin {\mathbb{N}^*}\)
c) \(\frac{7}{9} \notin \mathbb{N}\)
d) \(100 \in \mathbb{N}\)

\(A=\frac{20n+13}{4n+3}=\frac{5\left(4n+3\right)-2}{4n+3}=5-\frac{2}{4n+3}\)
Để A nhỏ nhất thì \(\frac{2}{4n+3}\) lớn nhất => 4n +3 nhỏ nhất mà n là số tự nhiên nên 4n + 3 nhỏ nhất khi n nhỏ nhất => n = 0
Ta có:
A = 20n+13 / 4n+3 = 5( 4n + 3 ) - 2/ 4n+3 = 5 - 2/ 4n +3
Để A nhỏ nhất thì 2/ 4n +3 lớn nhất
Suy ra 4n+3 nhỏ nhất <=> 4n + 3 là số tự nhiên nhỏ nhất
+) 4n + 3 = 0 => n = -3/ 4 ( loại vì n E N )
+) 4n + 3 = 1 => n = -1/ 2 ( loại vì n E N )
+) 4n + 3 = 2 => n = -1/ 4 ( loại vì n E N )
+) 4n + 3 = 3 => n = 0 ( thỏa mãn )
Vậy n = 0 thì A đạt giá trị lớn nhất .

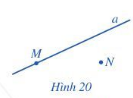
a) Điểm M thuộc đường thẳng a.
Điểm N không thuộc đường thẳng a.
b) N ∉ a.
M ∈ a.

a) A = {100;101;102;....} ----> A có vô số phần tử
B = {\(\phi\)} ----> B không có phần tử nào
C = {0;2;4;6;8;10;....} ----> C có vô số phần tử
D có 6 phần tử
b) B có là con của A
c) C không là con của A vì: 0 \(\in\) C nhưng 0 không thuộc A



NN là gì vậy ?
có một chữ N thôi tớ lộn