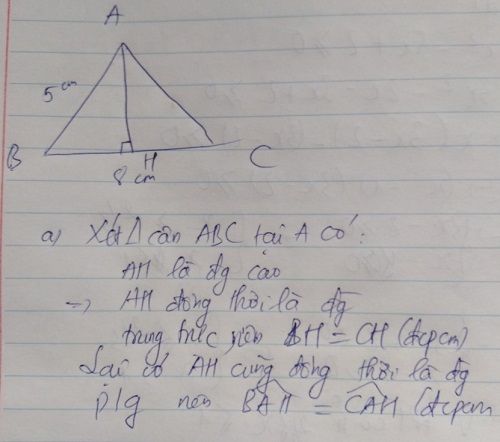Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

câu a theo hình của mình thì làm được rồi nhưng câu b mtheo hình của mình thì lại thấy kì kì bạn thử vẽ hình hộ mình được không
a) Xét ΔADI và ΔAHI , có :
ID = IH ( I là trung điểm của DH )
IA chung
góc AID = góc AIH = 90o
=> ΔADI = ΔAHI (c.g.c)

a) Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC(ΔABC cân tại A)
\(\widehat{A}\) chung
Do đó: ΔABH=ΔACK(cạnh huyền-góc nhọn)
⇒AH=AK(hai cạnh tương ứng)
b) Xét ΔAKI vuông tại K và ΔAHI vuông tại H có
AI là cạnh chung
AK=AH(cmt)
Do đó: ΔAKI=ΔAHI(cạnh huyền-cạnh góc vuông)
⇒\(\widehat{KAI}=\widehat{HAI}\)(hai góc tương ứng)
hay \(\widehat{BAI}=\widehat{CAI}\)
mà tia AI nằm giữa hai tia AB,AC
nên AI là tia phân giác của \(\widehat{BAC}\)(đpcm)
c) Xét ΔKBI vuông tại K và ΔHCI vuông tại H có
KI=HI(ΔAKI=ΔAHI)
\(\widehat{KIB}=\widehat{HIC}\)(hai góc đối đỉnh)
Do đó: ΔKBI=ΔHCI(cạnh góc vuông-góc nhọn kề)
⇒IB=IC(hai cạnh tương ứng)
Xét ΔIBC có IB=IC(cmt)
nên ΔIBC cân tại I(định nghĩa tam giác cân)
d) Ta có: AB=AC(ΔABC cân tại A)
nên A nằm trên đường trung trực của BC(tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: IB=IC(cmt)
nên I nằm trên đường trung trực của BC(tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra AI là đường trung trực của BC
hay AI⊥BC(đpcm)