K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
WR
24 tháng 6 2019
do hàm \(\cos x,\sin x\)luôn xđ trên R nên:
a) Y xđ \(\Leftrightarrow\frac{x+1}{x+2}xđ\Leftrightarrow x\ne-2\)\(\Rightarrow D=R\backslash\left\{-2\right\}\)
b) y xđ\(\Leftrightarrow x+4\ge0\Leftrightarrow x\ge-4\Rightarrow D=[-4,+\infty)\)
c) Y xđ \(\Leftrightarrow x^2-3x+2\ge0\Leftrightarrow\orbr{\begin{cases}x\ge2\\x\le1\end{cases}\Rightarrow}D=(-\infty,1]U[2,+\infty)\)
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 5 2020
a/ \(y'=42\left(2x+3\right)^{20}\left(x-4\right)^{23}+23\left(x-4\right)^{22}\left(2x+3\right)^{21}\)
b/ \(y=\frac{1}{x\sqrt{x}}=\frac{1}{\sqrt{x^3}}=x^{-\frac{3}{2}}\Rightarrow y'=-\frac{3}{2}x^{-\frac{5}{2}}=-\frac{3}{2x^2\sqrt{x}}\)
c/ \(y'=\frac{\left(x+\frac{1}{x}\right)'}{2\sqrt{\frac{x^2+1}{x}}}=\frac{1-\frac{1}{x^2}}{2\sqrt{\frac{x^2+1}{x}}}=\frac{\left(x^2-1\right)\sqrt{x}}{2x^2\sqrt{x^2+1}}\)
d/ \(y=x^2+x^{\frac{3}{2}}+1\Rightarrow y'=2x+\frac{3}{2}x^{\frac{1}{2}}=2x+\frac{3}{2}\sqrt{x}\)
e/ \(y'=\frac{\sqrt{1-x}+\frac{1+x}{2\sqrt{1-x}}}{1-x}=\frac{3-x}{2\left(1-x\right)\sqrt{1-x}}\)
f/ \(y'=\frac{\sqrt{a^2-x^2}+\frac{x^2}{\sqrt{a^2-x^2}}}{a^2-x^2}=\frac{a^2}{a^2-x^2}\)
7 tháng 3 2021
TH1: Nếu có 1 số bằng 0, giả sử là z, khi đó ta có \(x^4+y^4=1\)
và \(P=x^2+y^2\ge\sqrt{x^4+y^4}=1\)
Dấu '=' xảy ra khi 1 số =0, một số = \(\pm1\)
TH2: Nếu các số đều khác 0
Từ giả thiết => tồn tại tam giác ABC nhọn sao cho
\(x^2=\cos A,y^2=\cos B,z^2=\cos C\)
\(P=\cos A+\cos B+\cos C-\sqrt{2\cos A\cos B\cos C}\)
\(=1+4\sin\frac{A}{2}\sin\frac{B}{2}\sin\frac{C}{2}-\sqrt{2\cos A\cos B\cos C}\)
Ta chứng minh \(4\sin\frac{A}{2}\sin\frac{B}{2}\sin\frac{C}{2}\ge\sqrt{2\cos A\cos B\cos C}\) (1)
Ta có (1) \(\Leftrightarrow8\sin^2\frac{A}{2}\sin^2\frac{B}{2}\sin^2\frac{C}{2}\ge\cos A\cos B\cos C\)
\(\Leftrightarrow\frac{8\sin^2\frac{A}{2}\sin^2\frac{B}{2}\sin^2\frac{C}{2}}{\sin A\sin B\sin C}\ge\frac{\cos A\cos B\cos C}{\sin A\sin B\sin C}\)
\(\Leftrightarrow\cot A\cot B\cot C\le\tan\frac{A}{2}\tan\frac{B}{2}\tan\frac{C}{2}\)
\(\Leftrightarrow\tan A\tan B\tan C\ge\cot\frac{A}{2}\cot\frac{B}{2}\cot\frac{C}{2}\)
\(\Leftrightarrow\tan A+\tan B+\tan C\ge\cot\frac{A}{2}+\cot\frac{B}{2}+\cot\frac{C}{2}\) (2)
bđt (2) đúng vì \(\tan A+\tan B\ge2\cot\frac{C}{2}\) và 2 bđt tương tự
Dấu '=' xảy ra khi tam giác đều \(\Leftrightarrow x^2=y^2=z^2=\frac{1}{2}\)
\(\Rightarrow P\ge1\)
Dấu '=' xảy ra khi 2 số =0, một số \(=\pm1\) hoặc \(x^2=y^2=z^2=\frac{1}{2}\)
Vậy GTNN của P là 1
16 tháng 10 2020
Vì \(x\ge1\Rightarrow x^2\ge x\)
Từ đó: \(P\ge\frac{x}{\left(x+y\right)^2+x}+\frac{x}{z^2+x}=x\left[\frac{1}{\left(x+y\right)^2+x}+\frac{1}{z^2+x}\right]\)
\(\ge x\cdot\frac{4}{\left(x+y\right)^2+x+z^2+x}=\frac{4x}{\left(x+y\right)^2+z^2+2x}\) (Cauchy Schwarz)
Lại có: \(\left(x+y\right)^2+z^2=x^2+y^2+z^2+2xy=3\left(x+y+z\right)\)
\(\le3\sqrt{2\left[\left(x+y\right)^2+z^2\right]}\)
\(\Rightarrow\left(x+y\right)^2+z^2\le18\)
\(\Rightarrow P\ge\frac{4x}{18+2x}=2-\frac{18}{x+9}\ge2-\frac{18}{1+9}=\frac{1}{5}\)
Dấu "=" xảy ra khi: \(\hept{\begin{cases}x=1\\y=2\\z=3\end{cases}}\)
Vậy Min(P) = 1/5 khi x = 1 ; y = 2 ; z = 3
SG
2
6 tháng 4 2017
\(y'=x^2-6x\)
y' > 0 =>x<0;6<x
y' <3=>\(3-2\sqrt{3}< x< 3+2\sqrt{3}\)
BT
26 tháng 5 2017
\(y'\left(x\right)=3x^2-6x\).
a) \(y'\left(x\right)>0\)\(\Leftrightarrow3x^2-6x>0\)\(\Leftrightarrow\left[{}\begin{matrix}x< 0\\x>2\end{matrix}\right.\).
Vậy \(x< 0\) hoặc \(x>2\) thì \(y'\left(x\right)>0\).
b) \(y'\left(x\right)< 3\)\(\Leftrightarrow3x^2-6x< 3\)\(\Leftrightarrow3x^2-6x-3< 0\)\(\Leftrightarrow1-\sqrt{2}< x< 1+\sqrt{2}\).
Vậy \(1-\sqrt{2}< x< 1+\sqrt{2}\) thì \(y'\left(x\right)< 3\).
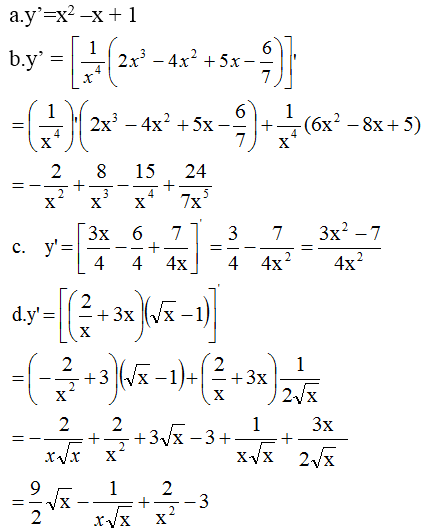
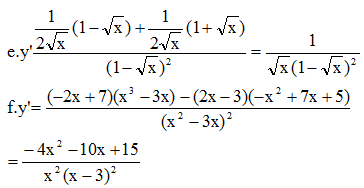
Lời giải:
$y=\frac{x-3}{x+4}\Rightarrow y'=\frac{7}{(x+4)^2}; y''=\frac{-14}{(x+4)^3}$
\(A=2\left[\frac{7}{(x+4)^2}\right]^2+(1-\frac{x-3}{x+4}).\frac{-14}{(x+4)^3}\)
\(=\frac{98}{(x+4)^4}-\frac{98}{(x+4)^4}=0\)