Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

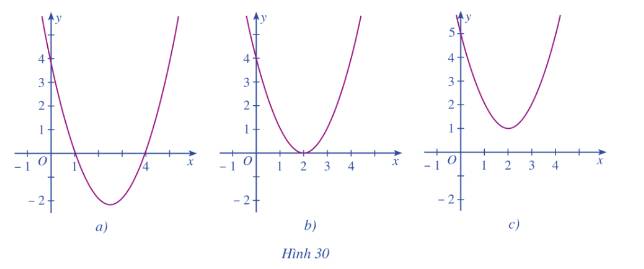
Hình 30a:
\(f\left( x \right) > 0\) có tập nghiệm là \(S = \left( { - \infty ;1} \right) \cup \left( {4; + \infty } \right)\)
\(f\left( x \right) < 0\) có tập nghiệm là \(S = \left( {1;4} \right)\)
\(f\left( x \right) \ge 0\) có tập nghiệm là \(S = \left( { - \infty ;1} \right] \cup \left[ {4; + \infty } \right)\)
\(f\left( x \right) \le 0\) có tập nghiệm là \(S = \left[ {1;4} \right]\)
Hình 30b:
\(f\left( x \right) > 0\) có tập nghiệm là \(S = \mathbb{R}\backslash \left\{ 2 \right\}\)
\(f\left( x \right) < 0\) có tập nghiệm là \(S = \emptyset \)
\(f\left( x \right) \ge 0\) có tập nghiệm là \(S = \mathbb{R}\)
\(f\left( x \right) \le 0\) có tập nghiệm là \(S = \left\{ 2 \right\}\)
Hình 30c:
\(f\left( x \right) > 0\) có tập nghiệm là \(S = \mathbb{R}\)
\(f\left( x \right) < 0\) có tập nghiệm là \(S = \emptyset \)
\(f\left( x \right) \ge 0\) có tập nghiệm là \(S = \mathbb{R}\)
\(f\left( x \right) \le 0\) có tập nghiệm là \(S = \emptyset \)

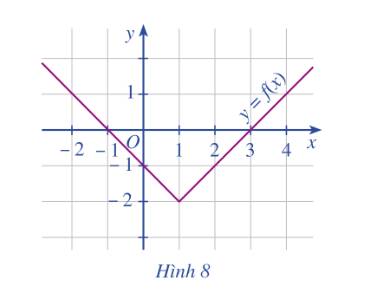
a) f(-2) = -1; f(-1) = 0; f(0) = 1; f(2) = 3
g(-1) = 0,5; g(-2) = 2; g(0) = 0
b) f(x) = 2 ⇒ x = 1
g(x) = 2 ⇒ x = 2 hoặc x = -2

a) Quan sát đồ thị:
điểm \(\left( {1; - 2} \right)\) (tức là có x =1; y=-2) thuộc đồ thị.
điểm \(\left( {2; - 1} \right)\) (tức là có x=2; y=-1) thuộc đồ thị hàm số.
điểm (0;0) không thuộc đồ thị hàm số.
b) Từ điểm trên Ox: \(x = 0\) ta kẻ đường thẳng song song với Oy ta được: \(f\left( 0 \right) = - 1\)
Từ điểm trên Ox: \(x = 3\) ta kẻ đường thẳng song song với Oy ta được: \(f\left( 3 \right) = 0\)
c) Giao điểm của đồ thị và trục Ox là điểm \(\left( {3;0} \right)\).

a, Bảng biến thiên:
Đồ thị hàm số:
b, \(f\left(x\right)>0\Leftrightarrow x\in\left(-\infty;-3\right)\cup\left(-1;+\infty\right)\)
\(f\left(x\right)< 0\Leftrightarrow x\in\left(-3;-1\right)\)
c, Yêu cầu bài toán là gì vậy:v
d, Phương trình hoành độ giao điểm của \(\left(P\right);\left(d\right)\):
\(x^2+4x+3=2x+m-5\)
\(\Leftrightarrow x^2+2x+8-m=0\)
\(\left(d\right)\) cắt \(\left(P\right)\) tại hai điểm phân biệt khi phương trình \(\left(1\right)\) có hai nghiệm phân biệt
\(\Delta'=1-\left(8-m\right)=m-7>0\Leftrightarrow m>7\)

a) Hệ số a là: a=1
\(f(0) = {0^2} - 4.0 + 3 = 3\)
\(f(1) = {1^2} - 4.1 + 3 = 0\)
\(f(2) = {2^2} - 4.2 + 3 = - 1\)
\(f(3) = {3^2} - 4.3 + 3 = 0\)
\(f(4) = {4^2} - 4.4 + 3 = 3\)
=> f(0); f(4) cùng dấu với hệ số a; f(2) khác dấu với hệ số a
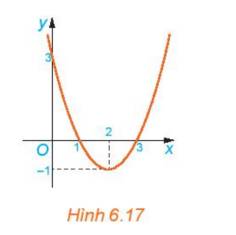
b) Nhìn vào đồ thị ta thấy
- Trên khoảng \(\left( { - \infty ;1} \right)\) đồ thị nằm phía trên trục hoành
- Trên khoảng \(\left( {1;3} \right)\), đồ thị nằm phía dưới trục hoành
- Trên khoảng \(\left( {3; + \infty } \right)\), đồ thị nằm phía trên trục hoành
c) - Trên khoảng \(\left( { - \infty ;1} \right)\) đồ thị nằm phía trên trục hoành => f(x)>0, cùng dầu với hệ số a
- Trên khoảng \(\left( {1;3} \right)\), đồ thị nằm phía dưới trục hoành => f(x) <0, khác dấu với hệ số a
- Trên khoảng \(\left( {3; + \infty } \right)\), đồ thị nằm phía trên trục hoành => f(x)>0, cùng dấu với hệ số a

a) Với \(x\in\left[0;1\right]\) => x - 2 < 0 => |x - 2| = - (x -2)
Khi đó, \(f\left(x\right)=2\left(m-1\right)x+\frac{m\left(x-2\right)}{-\left(x-2\right)}=2\left(m-1\right)x-m\)
Để f(x) < 0 với mọi \(x\in\left[0;1\right]\) <=> \(2\left(m-1\right)x-m

a)
\(f\left( { - 2} \right) = {\left( { - 2} \right)^2} = 4;\)\(f\left( { - 1} \right) = {\left( { - 1} \right)^2} = 1\)
\( \Rightarrow f\left( { - 2} \right) > f\left( { - 1} \right)\)
Lấy \({x_1},{x_2} \in \left( { - 2; - 1} \right)\) sao cho \({x_1} < {x_2}\).
\( \Rightarrow {x_1} - {x_2} < 0\)
\({x_1},{x_2} < 0 \Rightarrow {x_1} + {x_2} < 0\)
Ta có:
\(\begin{array}{l}f\left( {{x_1}} \right) = x_1^2;f\left( {{x_2}} \right) = x_2^2\\f\left( {{x_1}} \right) - f\left( {{x_2}} \right) = x_1^2 - x_2^2\\ = \left( {{x_1} - {x_2}} \right).\left( {{x_1} + {x_2}} \right) > 0\\ \Rightarrow f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\end{array}\)
=> Hàm số nghịch biến trên (-2;-1)
Vậy hàm số giảm khi x tăng từ -2 đến -1
b)
\(\begin{array}{l}f\left( 1 \right) = 1;f\left( 2 \right) = {2^2} = 4\\ \Rightarrow f\left( 1 \right) < f\left( 2 \right)\end{array}\)
Lấy \({x_1},{x_2} \in \left( {1;2} \right)\) sao cho \({x_1} < {x_2}\).
\( \Rightarrow {x_1} - {x_2} < 0\)
\({x_1},{x_2} > 0 \Rightarrow {x_1} + {x_2} > 0\)
Ta có:
\(\begin{array}{l}f\left( {{x_1}} \right) = x_1^2;f\left( {{x_2}} \right) = x_2^2\\f\left( {{x_1}} \right) - f\left( {{x_2}} \right) = x_1^2 - x_2^2\\ = \left( {{x_1} - {x_2}} \right).\left( {{x_1} + {x_2}} \right) < 0\\ \Rightarrow f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\end{array}\)
=> Hàm số đồng biến trên (1;2)
Vậy hàm số tăng khi x tăng từ 1 đến 2.

a, (from geogebra :V)
b, (do không rõ, mình gộp cả 2 điều kiện nhé)
Dựa vào đồ thị, điều kiện của x sao cho \(0< f\left(x\right)< 1\) là \(1< x< 5\).
Chúc bạn học tốt nha .
.