K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

23 tháng 2 2016
\(M>\frac{x}{x+y+z+t}+\frac{y}{x+y+z+t}+\frac{z}{x+y+z+t}+\frac{t}{x+y+z+t}=\frac{x+y+z+t}{x+y+z+t}=1\)
Mà \(\frac{a}{b}<1\) thì \(\frac{a}{b}<\frac{a+m}{b+m}\) ; \(m\in N\)*
Do đó \(M<\frac{x+t}{x+y+z+t}+\frac{y+z}{x+y+z+t}+\frac{z+x}{x+y+z+t}+\frac{t+y}{x+y+z+t}=\frac{2\left(x+y+z+t\right)}{x+y+z+t}=2\)
Vậy 1 < M < 2 nên M không phải là số tự nhiên/

CM
27 tháng 2 2019
Đáp án C.
Không tồn tại đường thẳng nào trong không gian cắt cả 4 đường thẳng đã cho
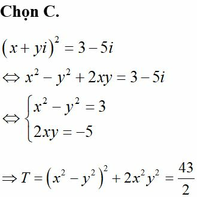


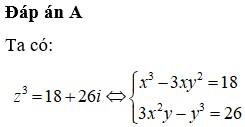

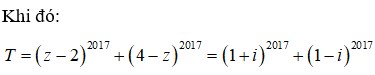
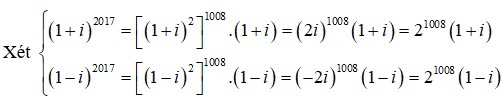


Đặt \(A=\frac{x}{x+y+z}+\frac{y}{x+y+t}+\frac{z}{y+z+t}+\frac{t}{x+z+t}\).Vì x,y,z,t E N nên:
\(\frac{x}{x+y+z+t}<\frac{x}{x+y+z}<\frac{x}{x+y}\)
\(\frac{y}{x+y+z+t}<\frac{y}{x+y+t}<\frac{y}{x+y}\)
\(\frac{z}{x+y+z+t}<\frac{z}{y+z+t}<\frac{z}{z+t}\)
\(\frac{t}{x+y+z+t}<\frac{t}{x+z+t}<\frac{t}{z+t}\)
do đó \(\frac{x}{x+y+z+t}+\frac{y}{x+y+z+t}+\frac{z}{x+y+z+t}+\frac{t}{x+y+z+t}\)<A<\(\left(\frac{x}{x+y}+\frac{y}{x+y}\right)+\left(\frac{z}{z+t}+\frac{t}{z+t}\right)\)
<=>1<A<2
vậy A ko phải là số nguyên
C cần gấp ko? T giải cho