Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng bất đẳng thức Cauchy :
\(\frac{x^4}{y^2\left(x+z\right)}+\frac{y^2}{2x}+\frac{x+z}{4}\ge3\sqrt[3]{\frac{x^4\cdot y^2\cdot\left(x+z\right)}{y^2\cdot\left(x+z\right)\cdot2x\cdot4}}=3\sqrt[3]{\frac{x^3}{8}}=\frac{3x}{2}\)
Tương tự ta cũng có :
\(\frac{y^4}{z^2\left(x+y\right)}+\frac{z^2}{2y}+\frac{x+y}{4}\ge\frac{3y}{2}\)
\(\frac{z^4}{x^2\left(y+z\right)}+\frac{x^2}{2z}+\frac{y+z}{4}\ge\frac{3z}{2}\)
Cộng theo vế ta được :
\(VT+\left(\frac{y^2}{2x}+\frac{z^2}{2y}+\frac{x^2}{2z}\right)+\frac{2\left(x+y+z\right)}{4}\ge\frac{3x}{2}+\frac{3y}{2}+\frac{3z}{2}\)
\(\Leftrightarrow VT+\frac{1}{2}\left(\frac{y^2}{x}+\frac{z^2}{y}+\frac{x^2}{z}\right)+\frac{1}{2}\left(x+y+z\right)\ge\frac{3}{2}\left(x+y+z\right)\)
\(\Leftrightarrow VT+\frac{1}{2}\cdot\frac{\left(x+y+z\right)^2}{x+y+z}+\frac{1}{2}\left(x+y+z\right)\ge\frac{3}{2}\left(x+y+z\right)\)
\(\Leftrightarrow VT+\frac{1}{2}\left(x+y+z\right)+\frac{1}{2}\left(x+y+z\right)\ge\frac{3}{2}\left(x+y+z\right)\)
\(\Leftrightarrow VT\ge\frac{x+y+z}{2}\)
Dấu "=" xảy ra \(\Leftrightarrow x=y=z\)

Lời giải:
Vì $xy+yz+xz=1$ nên:
\(x^2+1=x^2+xy+yz+xz=(x+y)(x+z)\)
\(y^2+1=y^2+xy+yz+xz=(y+x)(y+z)\)
\(z^2+1=z^2+xy+yz+xz=(z+y)(z+x)\)
Do đó:
\(\frac{x}{x^2+1}+\frac{y}{y^2+1}+\frac{z}{1+z^2}=\frac{x}{(x+y)(x+z)}+\frac{y}{(y+x)(y+z)}+\frac{z}{(z+x)(z+y)}\)
\(=\frac{x(y+z)+y(x+z)+z(x+y)}{(x+y)(y+z)(x+z)}=\frac{2(xy+yz+xz)}{(x+y)(y+z)(x+z)}=\frac{2}{\sqrt{(x+y)^2(y+z)^2(x+z)^2}}\)
\(=\frac{2}{\sqrt{(x+y)(x+z)(y+z)(y+x)(z+x)(z+y)}}=\frac{2}{\sqrt{(x^2+1)(y^2+1)(z^2+1)}}\) (đpcm)
Lời giải:
Vì $xy+yz+xz=1$ nên:
\(x^2+1=x^2+xy+yz+xz=(x+y)(x+z)\)
\(y^2+1=y^2+xy+yz+xz=(y+x)(y+z)\)
\(z^2+1=z^2+xy+yz+xz=(z+y)(z+x)\)
Do đó:
\(\frac{x}{x^2+1}+\frac{y}{y^2+1}+\frac{z}{1+z^2}=\frac{x}{(x+y)(x+z)}+\frac{y}{(y+x)(y+z)}+\frac{z}{(z+x)(z+y)}\)
\(=\frac{x(y+z)+y(x+z)+z(x+y)}{(x+y)(y+z)(x+z)}=\frac{2(xy+yz+xz)}{(x+y)(y+z)(x+z)}=\frac{2}{\sqrt{(x+y)^2(y+z)^2(x+z)^2}}\)
\(=\frac{2}{\sqrt{(x+y)(x+z)(y+z)(y+x)(z+x)(z+y)}}=\frac{2}{\sqrt{(x^2+1)(y^2+1)(z^2+1)}}\) (đpcm)

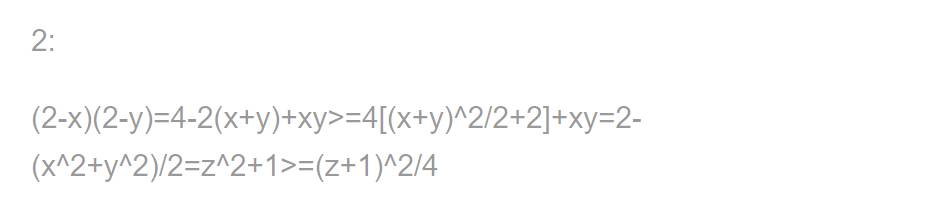
Tương tự, ta được:
\(\left(2-y\right)\left(2-z\right)>=\dfrac{\left(x+1\right)^2}{4}\)
và \(\left(2-z\right)\left(2-x\right)>=\left(\dfrac{y+1}{2}\right)^2\)
=>8(2-x)(2-y)(2-z)>=(x+1)(y+1)(z+1)
(x+yz)(y+zx)<=(x+y+yz+xz)^2/4=(x+y)^2*(z+1)^2/4<=(x^2+y^2)(z+1)^2/4
Tương tự, ta cũng co:
\(\left(y+xz\right)\left(z+y\right)< =\dfrac{\left(y^2+z^2\right)\left(x+1\right)^2}{2}\)
và \(\left(z+xy\right)\left(x+yz\right)< =\dfrac{\left(z^2+x^2\right)\left(y+1\right)^2}{2}\)
Do đó, ta được:
\(\left(x+yz\right)\left(y+zx\right)\left(z+xy\right)< =\left(x+1\right)\left(y+1\right)\left(z+1\right)\)
=>ĐPCM

\(VP=\left(2-x\right)\left(2-z\right)\left(2-y\right)=\left(y+z\right)\left(x+y\right)\left(2-y\right)\le\frac{\left(x+2y+z\right)^2}{4}\left(2-y\right)\)
\(VP\le\left(x+2y+z\right).\frac{\left(x+2y+z\right)\left(2-y\right)}{4}\le\left(x+2y+z\right)\frac{\left(x+y+z+2\right)^2}{16}=x+2y+z\)
Dấu "=" xảy ra khi \(\left\{{}\begin{matrix}x=z=1\\y=0\end{matrix}\right.\)

Để ý đẳng thức : \(\dfrac{xy}{\left(y-z\right)\left(z-x\right)}+\dfrac{yz}{\left(z-x\right)\left(x-y\right)}+\dfrac{xz}{\left(x-y\right)\left(y-z\right)}=\dfrac{xy\left(x-y\right)+yz\left(y-z\right)+xz\left(z-x\right)}{\left(x-y\right)\left(y-z\right)\left(z-x\right)}=-\dfrac{\left(x-y\right)\left(y-z\right)\left(z-x\right)}{\left(x-y\right)\left(y-z\right)\left(z-x\right)}=-1\)
Ta luôn có: \(\left(\dfrac{x}{y-z}+\dfrac{y}{z-x}+\dfrac{z}{x-y}\right)^2\ge0\) ;\(\forall x;y;z\)
\(\Leftrightarrow\dfrac{x^2}{\left(y-z\right)^2}+\dfrac{y^2}{\left(z-x\right)^2}+\dfrac{z^2}{\left(x-y\right)^2}\ge-2\sum\dfrac{xy}{\left(y-z\right)\left(z-x\right)}=2\)
(ĐPcm)
Dấu = xảy ra khi \(\dfrac{x}{y-z}+\dfrac{y}{z-x}+\dfrac{z}{x-y}=0\)
Thêm 1 ý tưởng đc buff từ cách trước :))
\(BDT\LeftrightarrowΣ\dfrac{x^2}{\left(y-z\right)^2}-2=\left(Σ\dfrac{x}{y-z}\right)^2-2Σ\dfrac{xy}{\left(y-z\right)\left(z-x\right)}-2\)
\(=\dfrac{\left(Σ\left(x^3-x^2y-x^2z+xyz\right)\right)^2}{\prod\left(x-y\right)^2}-2\dfrac{Σ\left(x^2y-x^2z\right)}{\prod\left(x-y\right)}-2\)
\(=\dfrac{\left(Σ\left(x^3-x^2y-x^2z+xyz\right)\right)^2}{\prod\left(x-y\right)^2}\ge0\)

\(P=3x^2+3z^2+10y^2+10t^2+8xy+8zt+4zx+2yz+2xt\)
\(P\le5x^2+5z^2+10y^2+10t^2+8xy+8zt+2yz+2xt\)
\(P\le10+5y^2+5t^2+8xy+8zt+2yz+2xt\)
\(\left\{{}\begin{matrix}8xy=\left(2+2\sqrt{5}\right)\left[2.x.\frac{\left(\sqrt{5}-1\right)}{2}y\right]\le\left(2+2\sqrt{5}\right)\left[x^2+\left(\frac{3-\sqrt{5}}{2}\right)y^2\right]\\8zt\le\left(2+2\sqrt{5}\right)\left[z^2+\left(\frac{3-\sqrt{5}}{2}\right)t^2\right]\\2yz\le\left(\frac{\sqrt{5}+1}{2}\right)\left[z^2+\left(\frac{3-\sqrt{5}}{2}\right)y^2\right]\\2xt\le\left(\frac{\sqrt{5}+1}{2}\right)\left(x^2+\left(\frac{3-\sqrt{5}}{2}\right)t^2\right)\end{matrix}\right.\)
\(\Rightarrow P\le10+\frac{5}{2}\left(\sqrt{5}+1\right)\left(x^2+y^2+z^2+t^2\right)\le15+5\sqrt{5}\)
Dấu "=" xảy ra khi và chỉ khi: \(\left\{{}\begin{matrix}x=z=\sqrt{\frac{5-\sqrt{5}}{10}}\\y=t=\sqrt{\frac{5+\sqrt{5}}{10}}\end{matrix}\right.\)
Chắc bạn ghi nhầm đề, phải là \(x^3-y^3-z^3=y^2\left(x-y\right)+z^2\left(x-z\right)\)
Ta có:
\(y^2\left(x-y\right)+z^2\left(x-z\right)=xy^2-y^3+xz^2-z^3\)
\(=x\left(y^2+z^2\right)-y^3-z^3\)
\(=x.x^2-y^3-z^3\)
\(=x^3-y^3-z^3\) (đpcm)