Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B.
Từ giả thiết, suy ra
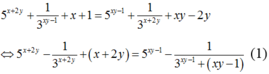
Xét hàm số f ( t ) = 5 t - 1 3 t + t trên ℝ .
Đạo hàm f ' ( t ) = 5 t . ln 5 - ln 3 3 t + 1 > 0 , ∀ t ∈ ℝ ⇒ hàm số f ( t ) luôn đồng biến trên ℝ .
Suy ra
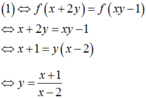
Do y > 0 nên x + 1 x - 2 > 0 ⇔ [ x > 2 x < - 1 . Mà x > 0 nên x > 2 .
Từ đó T = x + y = x + x + 1 x - 2 . Xét hàm số g ( x ) = x + x + 1 x - 2 trên 2 ; + ∞ .
Đạo hàm
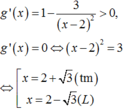
Lập bảng biến thiên của hàm số trên 2 ; + ∞ , ta thấy min g ( x ) = g ( 2 + 3 ) = 3 + 2 3 .
Vậy T m i n = 3 + 2 3 khi x = 2 + 3 và x = 1 + 3 .

Đặt \(x+y=t,t\in\left[-2;2\right]\)
Biến đổi được \(P=-2t^3+6t\)
Xét \(f\left(t\right)=-2t^3+6t\) trên \(\left[-2;2\right]\)
Lập bảng biến thiên
Ta có \(P_{Max}=4\) khi t=1
\(P_{Min}=-4\) khi t= -1

Từ giả thiết ta suy ra
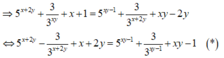
Xét hàm số f ( t ) = 5 t - 1 3 t + t với t ∈ ℝ , f ' ( t ) = 5 t . ln 5 + 3 - t . ln 3 + 1 > 0 ; ∀ t ∈ ℝ
Suy ra y= f( t) là hàm số đồng biến trên R mà từ ( * ) suy ra
f (x+ 2y) =f( xy-1) hay x+ 2y= xy-1
![]()
với x>0 suy ra y>1.
Khi đó
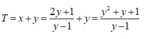
Xét hàm số
f ( y ) = y 2 + y + 1 y - 1 t r ê n 1 ; + ∞ f ' y = y 2 - 2 y - 2 y - 1 2 = 0 ⇔ y = ± 1 + 3 f 1 + 3 = 3 + 2 3 ; lim y → 1 f ( y ) = lim y → + ∞ f ( y ) = + ∞
Do đó, giá trị nhỏ nhất của hàm số là 3 + 2 3 .
Vậy kết quả là 3 + 2 3
Chọn B.

Bài này thì chia 2 vế của giả thiết cho z2 ta thu được:
\(\frac{x}{z}+2.\frac{x}{z}.\frac{y}{z}+\frac{y}{z}=4\Leftrightarrow a+2ab+b=4\)
(đặt \(a=\frac{x}{z};b=\frac{y}{z}\)).Mà ta có: \(4=a+2ab+b\le a+b+\frac{\left(a+b\right)^2}{2}\Rightarrow a+b\ge2\) Lại có:
\(P=\frac{\left(\frac{x}{z}+\frac{y}{z}\right)^2}{\left(\frac{x}{z}+\frac{y}{z}\right)^2+\left(\frac{x}{z}+\frac{y}{z}\right)}+\frac{3}{2}.\frac{1}{\left(\frac{x}{z}+\frac{y}{z}+1\right)^2}\) (chia lần lượt cả tử và mẫu của mỗi phân thức cho z2)
\(=\frac{\left(a+b\right)^2}{\left(a+b\right)^2+\left(a+b\right)}+\frac{3}{2\left(a+b+1\right)^2}\).. Tiếp tục đặt \(t=a+b\ge2\) thu được:
\(P=\frac{t}{\left(t+1\right)}+\frac{3}{2\left(t+1\right)^2}=\frac{2t\left(t+1\right)+3}{2\left(t+1\right)^2}\)\(=\frac{2t^2+2t+3}{2\left(t+1\right)^2}-\frac{5}{6}+\frac{5}{6}\)
\(=\frac{2\left(t-2\right)^2}{12\left(t+1\right)^2}+\frac{5}{6}\ge\frac{5}{6}\)
Vậy...
P/s: check xem em có tính sai chỗ nào không:v

Do \(x^2+y^2=1\), đặt \(\left\{{}\begin{matrix}x=sina\\y=cosa\end{matrix}\right.\)
\(P=\left(3-sina\right)\left(3-cosa\right)=9-3\left(sina+cosa\right)+sina.cosa\)
Đặt \(sina+cosa=t\Rightarrow t\in\left[-\sqrt{2};\sqrt{2}\right]\)
\(t^2=1+2sina.cosa\Rightarrow sina.cosa=\dfrac{t^2-1}{2}\)
\(P=9-3t+\dfrac{t^2-1}{2}=\dfrac{1}{2}t^2-3t+\dfrac{17}{2}\)
Xét hàm \(f\left(t\right)=\dfrac{1}{2}t^2-3t+\dfrac{17}{2}\) trên \(\left[-\sqrt{2};\sqrt{2}\right]\)
\(f'\left(t\right)=t-3=0\Rightarrow t=3\notin\left[-\sqrt{2};\sqrt{2}\right]\)
\(f\left(-\sqrt{2}\right)=\dfrac{19+6\sqrt{2}}{2}\) ; \(f\left(\sqrt{2}\right)=\dfrac{19-6\sqrt{2}}{2}\)
\(\Rightarrow P_{min}=f\left(\sqrt{2}\right)=\dfrac{19-6\sqrt{2}}{2}\) khi \(t=\sqrt{2}\)

Đáp án C.
Ta có: GT
<=> 5x+2y + x + 2y – 3–x–2y = 5xy–1 – 31–xy + xy – 1.
X é t h à m s ố f t = 5 t + t - 3 - t
⇒ f t = 5 t ln 5 + 1 + 3 - t ln 3 > 0 ∀ t ∈ ℝ
Do đó hàm số đồng biến trên ℝ suy ra
f(x+2y) = f(xy – 1) <=> x+ 2y = xy – 1
⇔ x = 2 y + 1 y - 1 ⇒ T = 2 y + 1 y - 1 + y .
Do x > 0 => y > 1.
Ta có:
T = 2 + y + 3 y - 1 = 3 + y - 1 + 3 y - 1 ≥ 3 + 2 3 .

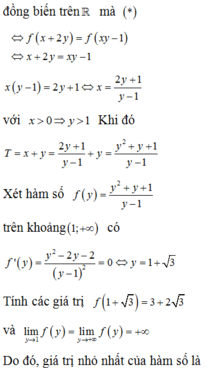
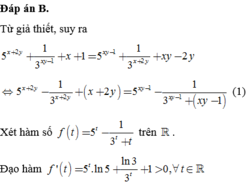
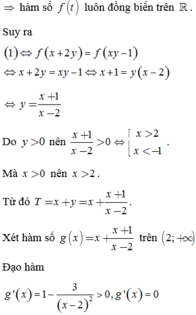

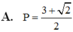
\(P=xy-3\left(x+y\right)+9\)
Đặt \(x+y=a\Rightarrow1< a\le\sqrt{2}\)
\(a^2=x^2+y^2+2xy=1+2xy\Rightarrow xy=\frac{a^2-1}{2}\)
\(P=\frac{a^2-1}{2}-3a+9\Rightarrow2P=a^2-6a+17\)
\(2P=a^2-6a-2+6\sqrt{2}+19-6\sqrt{2}\)
\(2P=\left(a+\sqrt{2}\right)\left(a-\sqrt{2}\right)-6\left(a-\sqrt{2}\right)+19-6\sqrt{2}\)
\(2P=\left(\sqrt{2}-a\right)\left(6-\sqrt{2}-a\right)+19-6\sqrt{2}\ge19-6\sqrt{2}\)
\(\Rightarrow P\ge\frac{19-6\sqrt{2}}{2}\)
Dấu "=" xảy ra khi \(a=\sqrt{2}\) hay \(x=y=\frac{\sqrt{2}}{2}\)