
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Ta có: \(a^2+2a-4=0\)
\(\Leftrightarrow\left(\sqrt{5}-1\right)^2+2\left(\sqrt{5}-1\right)-4=0\)
\(\Leftrightarrow6-2\sqrt{5}+2\sqrt{5}-2-4=0\)
\(\Leftrightarrow0=0\)(đúng)
b) Ta có: \(\left(a^3+2a^4-4a+2\right)^{10}\)
\(=\left[a\left(a^2+2a-4\right)+2\right]^{10}\)
\(=2^{10}=1024\)

http://olm.vn/hoi-dap/question/104313.html
coi hỉu j ko tui đang mò

\(x=\frac{1}{2}\sqrt{\sqrt{2}+\frac{1}{8}}-\frac{1}{8}\sqrt{2}\)
\(\Leftrightarrow x+\frac{\sqrt{2}}{8}=\frac{1}{2}\sqrt{\sqrt{2}+\frac{1}{8}}\)
\(\Leftrightarrow\left(x+\frac{\sqrt{2}}{8}\right)^2=\frac{1}{4}\left(\sqrt{2}+\frac{1}{8}\right)\)
\(\Leftrightarrow x^2+\frac{x\sqrt{2}}{4}+\frac{1}{32}=\frac{\sqrt{2}}{4}+\frac{1}{32}\)
\(\Leftrightarrow x^2+\frac{x\sqrt{2}}{4}-\frac{\sqrt{2}}{4}=0\)
\(\Leftrightarrow4x^2+x\sqrt{2}-\sqrt{2}=0\)(1)
\(\Leftrightarrow x\sqrt{2}=\sqrt{2}-4x^2\)
\(\Leftrightarrow x=1-2x^2\sqrt{2}\)
Thay vào M ta sẽ được
\(M=x^2+\sqrt{x^4+1-2x^2\sqrt{2}+1}\)
\(=x^2+\sqrt{\left(x^2-\sqrt{2}\right)^2}\)
\(=x^2+\left|x^2-\sqrt{2}\right|\)
Từ \(\left(1\right)\Rightarrow\sqrt{2}-x\sqrt{2}=4x^2\ge0\)
\(\Leftrightarrow\sqrt{2}\left(1-x\right)\ge0\)
\(\Leftrightarrow x\le1\)
\(\Leftrightarrow x^2\le1< \sqrt{2}\)
\(\Rightarrow\left|x^2-\sqrt{2}\right|=\sqrt{2}-x^2\)
Khi đó \(M=x^2+\left|x^2-\sqrt{2}\right|=x^2-\sqrt{2}+x^2=\sqrt{2}\)
|N|

\(A=\dfrac{x-9}{3+\sqrt{x}}\) (đề như này pk?)
a) Để A có nghĩa \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\3+\sqrt{x}\ne0\left(lđ\right)\end{matrix}\right.\)\(\Rightarrow x\ge0\)
b) \(A=\dfrac{x-9}{3+\sqrt{x}}=\dfrac{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}{3+\sqrt{x}}=\sqrt{x}-3\)
c) Với x=0 (tmđk) thay vào A ta được: \(A=\sqrt{0}-3=-3\)
Với x=-1 (ktm đk)
Với x=16 (tmđk) thay vào A ta được: \(A=\sqrt{16}-3=1\)
d) \(A\in Z\Leftrightarrow\sqrt{x}-3\in Z\Leftrightarrow\sqrt{x}\in Z\) \(\Leftrightarrow\) x là số chính phương

\(\Delta'=\left(-\sqrt{5}\right)^2-1.2=5-2=3>0\)
Suy ra pt luôn có 2 nghiệm phân biệt
Áp dụng định lý Vi-ét ta có:\(\left\{{}\begin{matrix}x_1+x_2=2\sqrt{5}\\x_1x_2=2\end{matrix}\right.\)
\(E=\dfrac{x^2_1+x_1x_2+x^2_2}{x^2_1+x^2_2}\\
=\dfrac{\left(x_1+x_2\right)^2-x_1x_2}{\left(x_1+x_2\right)^2-2x_1x_2}\\
=\dfrac{\left(2\sqrt{5}\right)^2-2}{\left(2\sqrt{5}\right)^2-2.2}\\
=\dfrac{20-2}{20-4}\\
=\dfrac{18}{16}\\
=\dfrac{9}{8}\)
\(E=\dfrac{\left(x_1+x_2\right)^2-x_1x_2}{\left(x_1+x_2\right)^2-2x_1x_2}=\dfrac{4.5-2}{4.5-2.2}=\dfrac{18}{16}=\dfrac{9}{8}\)
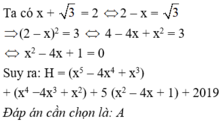
\(x+\sqrt{3}=2\Rightarrow\sqrt{3}=2-x\Rightarrow3=\left(2-x\right)^2\Rightarrow x^2-4x+1=0\)
Ta có:
\(B=x^5-4x^4+x^4-4x^3+x^3+5x^2+x^2-20x+5+2013\)
\(\Rightarrow B=x^5-4x^4+x^3+x^4-4x^3+x^2+5x^2-20x+5+2013\)
\(\Rightarrow B=x^3\left(x^2-4x+1\right)+x^2\left(x^2-4x+1\right)+5\left(x^2-4x+1\right)+2013\)
\(\Rightarrow B=x^3.0+x^2.0+5.0+2013=2013\)