Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

hình của mjnh thiếu điểm H và K rồi bạn tự thêm vào đi
a, tam giác MND cân tại M (gt)
=> ^MND = ^MDN (tc)
^MND + ^MNB = 180 (kb)
^MDN + ^MDA = 180 (kb)
=> ^MNB = ^MDA
xét tam giác MNB và tam giác MDA có BN = DA (gt)
MN = MD do tam giác MND cân tại M (gt)
=> tg MNB = tg MDA (c-g-c)
=> MA = MB (đn)
=> tg MAB cân tại M (Đn)
b, xét tam giác DHA và tam giác NKB có : AD = BN (gt)
^AHD = ^BKN = 90
^A = ^B do tam giác MAB cân tại M (câu a)
=> tg DHA = tg NKB (ch-gn)
=> DH = KN (đn)
c, tg DHA = tg NKB (câu b)
=> AH = KB (đn)
có MA = MB (câu a)
AH + MH = AM
MK + KB = BM
=> MH = MK
d, có ^HDA = ^KNB do tg DHA = tg NKB (Câu b)
^HDA = ^NDI (đối đỉnh)
^KNB = ^DNI (đối đỉnh)
=> ^NDI = ^DNI
=> tam giác DNI cân tại I

vẽ trên mt nên hình ko được đẹp ..
a, Xét \(\Delta OMN\perp N\)và \(\Delta OMP\perp P\)có :
\(\widehat{O_1}=\widehat{O_2}\)\(\left(gt\right)\)
\(OM\)cạnh chung
= > \(\Delta OMN=\Delta OMP\left(ch-gn\right)\)
b, Vì \(\Delta OMN=\Delta OMP\)( câu a, )
= > \(ON=OP\)( 2 cạnh tương ứng )
Xét \(\Delta ONP\)có :
\(ON=OP\left(cmt\right)\)
= > \(\Delta ONP\)là tam giác cân ( cân tại O )
a, Xét 2 tam giác vuông OMN và OMP có :
\(\widehat{O_1}=\widehat{O_2}\) ( gt )
OM cạnh chung
= > \(\Delta OMN=\Delta OMP\left(ch-gn\right)\)
b, Vì \(\Delta OMN=\Delta OMP\)( câu a,)
= > ON = OP
Xét \(\Delta ONP\)có :
\(ON=OP\left(cmt\right)\)
= > \(\Delta ONP\)là tam giác cân ( cân tại O )

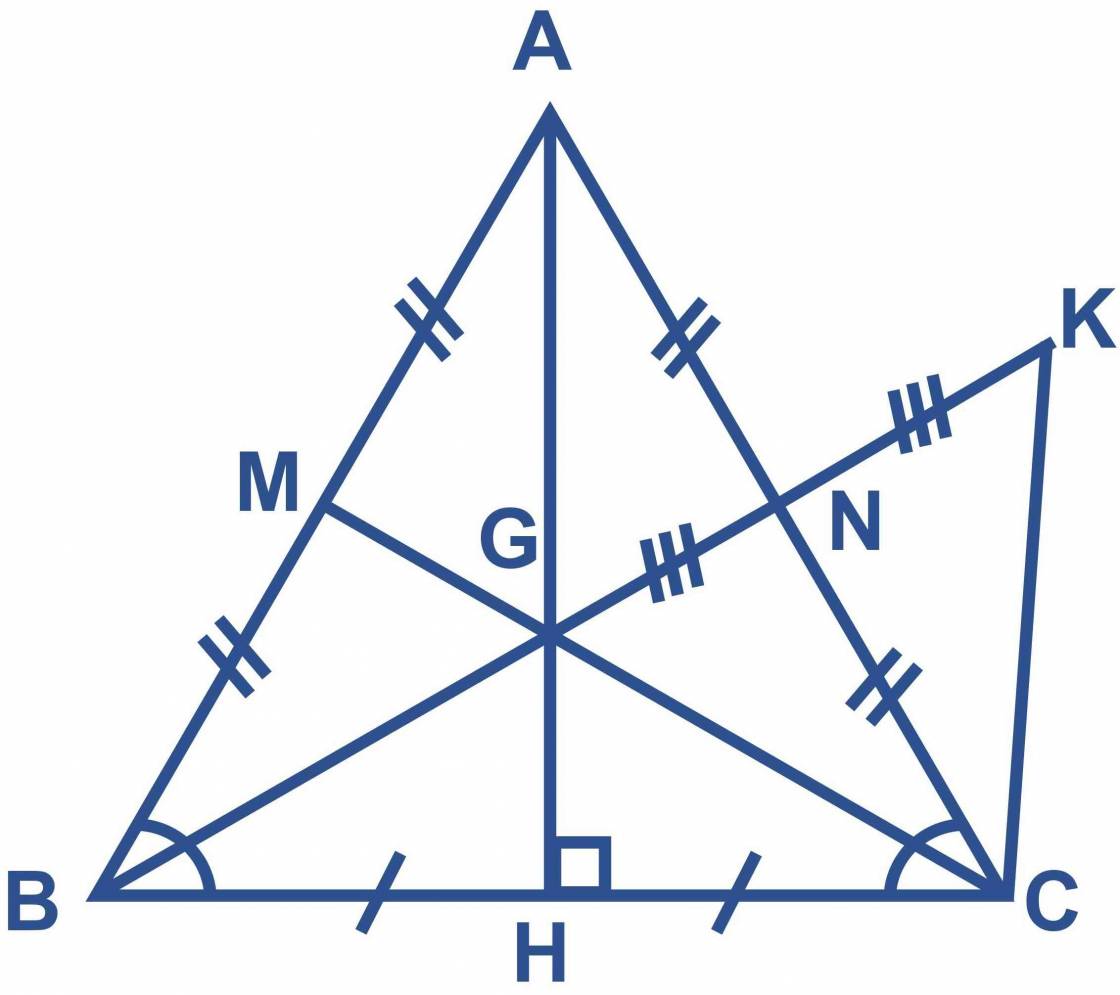
a) trong ΔABC, có góc AHB là góc vuông
góc ABH là góc nhọn
⇒ góc AHB > góc ABH
⇒ AB > AH
b) M là trung điểm của AB và N là trung điểm của AC, mà AB = AC (2 cạnh bên của tam giác cân) ⇒ MB = NC
xét tam giác MBC và tam giác NCB, ta có :
MB = NC (cmt)
góc B = góc C (2 góc đáy của 1 tam giác cân)
BC là cạnh chung
⇒ tam giác MBC = tam giác NCB (c-g-c)
⇒ MC = NB (2 cạnh tương ứng)
c) xét tam giác NAG và tam giác NCK , ta có :
NA = NC (vì N là trung điểm của cạnh AC)
góc NAG = góc NCK (đối đỉnh)
NG = NK (gt)
=> tam giác NAG = tam giác NCK (c-g-c)
=> AG = CK (2 cạnh tương ứng)

Bài 3:
a: Xét ΔAMB và ΔDMC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔAMB=ΔDMC
b: Xét tứ giác ABDC có
M là trung điểm của BC
M là trung điểm của AD
Do đó: ABDC là hình bình hành
Suy ra:AC//BD và AC=BD
c: Xét ΔABC và ΔDCB có
AB=DC
\(\widehat{ABC}=\widehat{DCB}\)
BC chung
Do đó: ΔABC=ΔDCB
Suy ra: \(\widehat{BAC}=\widehat{CDB}=90^0\)
a) ta có OM = ON (gt)
=> OMN cân tại O
b) vì OMN cân tại O mà góc MON = 60 độ
-> góc OMN=góc ONM = (180 - 60 ) : 2 = 60 độ
=> tan giác OMN đều
xét Tam giác OHM và tam giác OHN
có OM = ON (gt)
góc ONH = góc OMH (OMN là tam giác cân)
góc ONH = góc OMH (H là đường cao )
=> tam giác OHM = tam giác OHN ( g-c-g)
=> HM = HN ( 2 cạnh tương ứng )