Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đề bài sai, sửa đề: \(2\le\sqrt{x^2+y^2}+\sqrt{xy}\le\sqrt{6}\)
Đặt \(P=\sqrt{x^2+y^2}+\sqrt{xy}>0\)
\(\Rightarrow P^2=x^2+y^2+xy+2\sqrt{\left(x^2+y^2\right)xy}\ge x^2+y^2+xy+2\sqrt{2xy.xy}\)
\(\Rightarrow P^2\ge x^2+y^2+\left(2\sqrt{2}+1\right)xy\ge x^2+y^2+2xy=4\)
\(\Rightarrow P\ge2\)
Dấu "=" xảy ra khi \(\left(x;y\right)=\left(2;0\right);\left(0;2\right)\)
Lại có: \(P^2=x^2+y^2+xy+2\sqrt{\left(x^2+y^2\right)xy}=x^2+y^2+xy+\sqrt{4xy.\left(x^2+y^2\right)}\)
\(\Rightarrow P^2\le x^2+y^2+xy+\dfrac{1}{2}\left(4xy+x^2+y^2\right)=\dfrac{3}{2}\left(x+y\right)^2=6\)
\(\Rightarrow P\le\sqrt{6}\)
Dấu "=" xảy ra khi \(\left(x;y\right)=\left(\dfrac{3-\sqrt{3}}{3};\dfrac{3+\sqrt{3}}{3}\right)\)

Ta có: \(A=\left(\dfrac{x\sqrt{x}+y\sqrt{y}}{\sqrt{x}+\sqrt{y}}-\sqrt{xy}\right):\left(x-y\right)+\dfrac{2\sqrt{y}}{\sqrt{x}+\sqrt{y}}\)
\(=\dfrac{\left(x-2\sqrt{xy}+y\right)}{x-y}+\dfrac{2\sqrt{y}}{\sqrt{x}+\sqrt{y}}\)
\(=\dfrac{\sqrt{x}-\sqrt{y}+2\sqrt{y}}{\sqrt{x}+\sqrt{y}}\)
=1

1: \(A=\dfrac{x-2\sqrt{xy}+y}{x-y}=\dfrac{\left(\sqrt{x}-\sqrt{y}\right)^2}{\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)}=\dfrac{\sqrt{x}-\sqrt{y}}{\sqrt{x}+\sqrt{y}}\)
2: Thay \(x=3+2\sqrt{2}\) và \(y=3-2\sqrt{2}\) vào A, ta được:
\(A=\dfrac{\sqrt{2}+1-\sqrt{2}+1}{\sqrt{2}+1+\sqrt{2}-1}=\dfrac{2}{2\sqrt{2}}=\dfrac{\sqrt{2}}{2}\)

Ta có: \(A-3\)
\(=\dfrac{x+5-3\sqrt{x}-3}{\sqrt{x}+1}\)
\(=\dfrac{x-3\sqrt{x}+2}{\sqrt{x}+1}\ge0\forall x\) thỏa mãn ĐKXĐ
hay A\(\ge3\)

a: \(\sqrt{6+2\sqrt{5}}-\sqrt{6-2\sqrt{5}}\)
\(=\sqrt{5}+1-\sqrt{5}+1\)
=2
c: \(\dfrac{x-y}{\sqrt{x}-\sqrt{y}}=\sqrt{x}+\sqrt{y}\)
d: \(\dfrac{y-2\sqrt{y}+1}{\sqrt{y}-1}=\sqrt{y}-1\)

a: \(=x-\sqrt{xy}+y-x+2\sqrt{xy}-y=\sqrt{xy}\)
b: \(=\dfrac{1+\sqrt{a}}{a-\sqrt{a}}\cdot\dfrac{\left(\sqrt{a}-1\right)^2}{\sqrt{a}+1}=\dfrac{\sqrt{a}-1}{\sqrt{a}}\)

Đề bài chắc chắn là có vấn đề
Thử với \(x=y=z=\dfrac{1}{3}\) thì \(VT=\dfrac{\sqrt{2}}{4}< 2\)
Như bạn sửa điều kiện thành \(x^3+y^3+z^3=1\) thì dấu "=" không xảy ra
Việc chứng minh vế trái lớn hơn 2 (một cách tuyệt đối) khá đơn giản:
\(\dfrac{x^2}{\sqrt{1-x^2}}=\dfrac{x^3}{x\sqrt{1-x^2}}\ge\dfrac{x^3}{\dfrac{x^2+1-x^2}{2}}=2x^3\)
Làm tương tự với 2 số hạng còn lại, sau đó cộng vế
Nhưng đẳng thức không xảy ra.
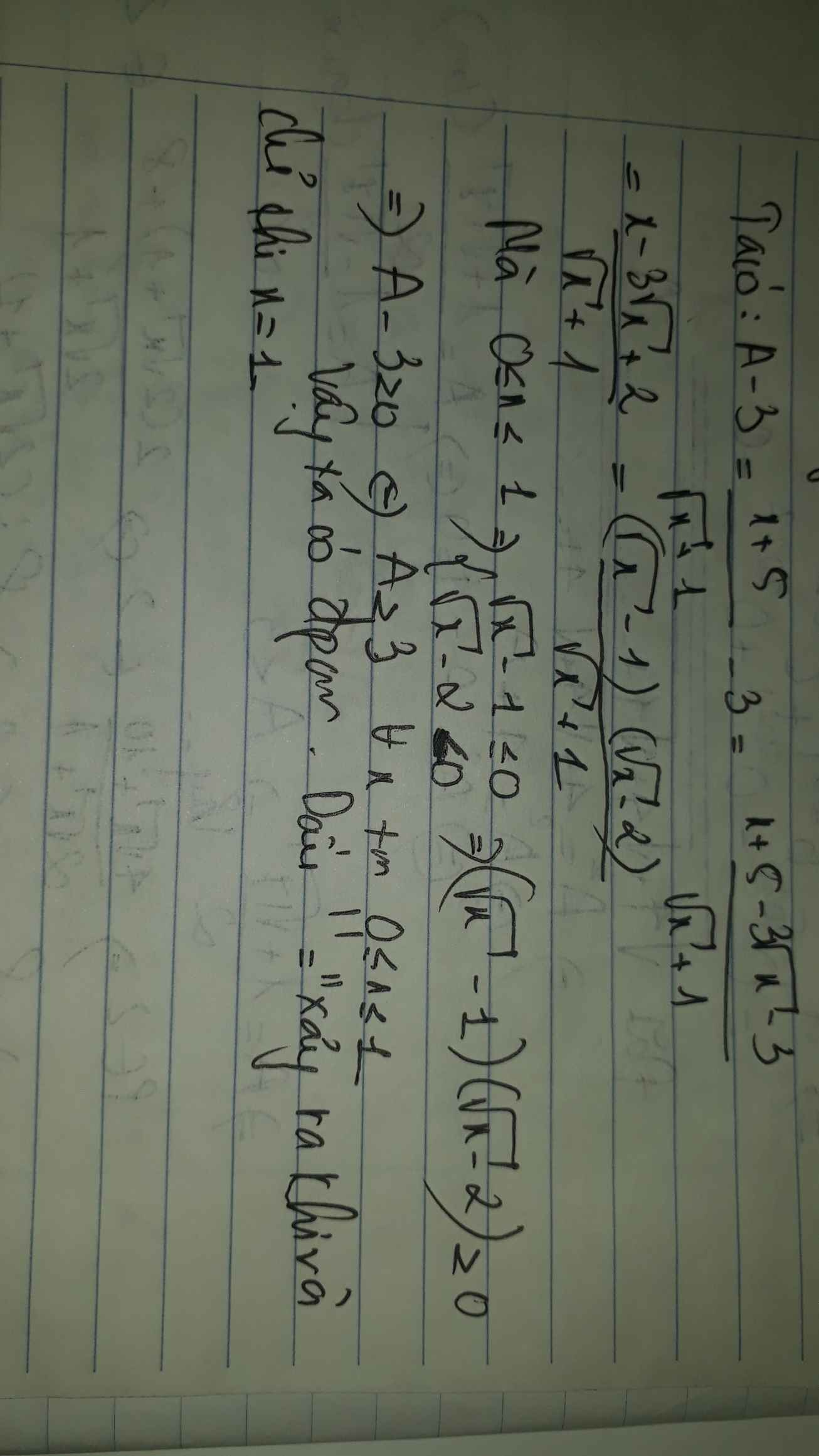
sai đề phải ko nhỉ,\(2\sqrt{x}+\sqrt{y}=1\) thì áp dụng Bunhiacopkxi,còn trừ thì mình chịu.
Áp dụng bất đẳng thức Bunhiacopxki ta có:
\(\left(2.\sqrt{x}+1.\sqrt{y}\right)^2\le\left(2^2+1^2\right)\left(x+y\right)\)
<=> \(5\left(x+y\right)\ge1\Leftrightarrow x+y\ge\dfrac{1}{5}\)
Dấu ''='' xảy ra <=> x=4/25 và y=1/25