Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tam giác AMD và tam giác AEN:
Góc A chung.
AM = AE (gt).
AD = AN (gt).
=> Tam giác AMD = Tam giác AEN (c - g - c).
=> MD = EN (2 cạnh tương ứng).
Ta có: \(\widehat{AMD}+\widehat{NMI}=180^o;\widehat{AEN}+\widehat{DEI}=180^o.\)
Mà \(\widehat{AMD}=\widehat{AEN}\) (Tam giác AMD = Tam giác AEN).
=> \(\widehat{NMI}=\widehat{DEI.}\)
Ta có: MN = AN = AM; ED = AD - AE.
Mà AM = AE, AN = AD (gt).
=> MN = ED.
Xét tam giác INM và tam giác IDE:
MN = ED (cmt).
\(\widehat{NMI}=\widehat{DEI}\left(cmt\right).\)
\(\widehat{MNI}=\widehat{EDI}\) (Tam giác AMD = Tam giác AEN).
=> Tam giác INM = Tam giác IDE (g - c - g).
Xét tam giác NAI và tam giác DAI:
AI chung.
AN = AD (gt).
NI = DI (Tam giác INM = Tam giác IDE).
=> Tam giác NAI = Tam giác DAI (c - c - c).
=> \(\widehat{NAI}=\widehat{DAI}\) (2 góc tương ứng).
=> AI là phân giác góc xAy.
Xét tam giác AND: AN = AD (gt).
=> Tam giác AND cân tại A.
Mà AI là phân giác (cmt).
=> AI là đường cao (Tính chất tam giác cân).
=> AI vuông góc với NB

a: Xét ΔABE và ΔADC có
AB=AD
\(\widehat{BAE}\) chung
AE=AC
DO đó: ΔABE=ΔADC
Suy ra: BE=DC
b: Xét ΔIBC và ΔIDE có
\(\widehat{IBC}=\widehat{IDE}\)
BC=DE
\(\widehat{ICB}=\widehat{IED}\)
Do đó: ΔIBC=ΔIDE
c: Xét ΔAIC và ΔAIE có
AI chung
IC=IE
AC=AE
DO đó: ΔAIC=ΔAIE
Suy ra: \(\widehat{CAI}=\widehat{EAI}\)
hay AI là tia phân giác của góc xAy

a) Ta có:
AE=AB+BE
AC=AD+DC
mà AD=AB ; BE=DC
=>AE=AC
Xét tam giác ABC và tam giác ADE có:
AD=AB
A là góc chung
AE= AC
=> Tam giác ABC = tam giác ADE
b) Ta có
Tam giác ABC = tam giâc ADE
=> Góc AED=góc ACB (2 góc tương ứng)
=>BC=DE ( 2 cạnh tương ứng)
c) Đến đây thì mình chịu. Sorry!

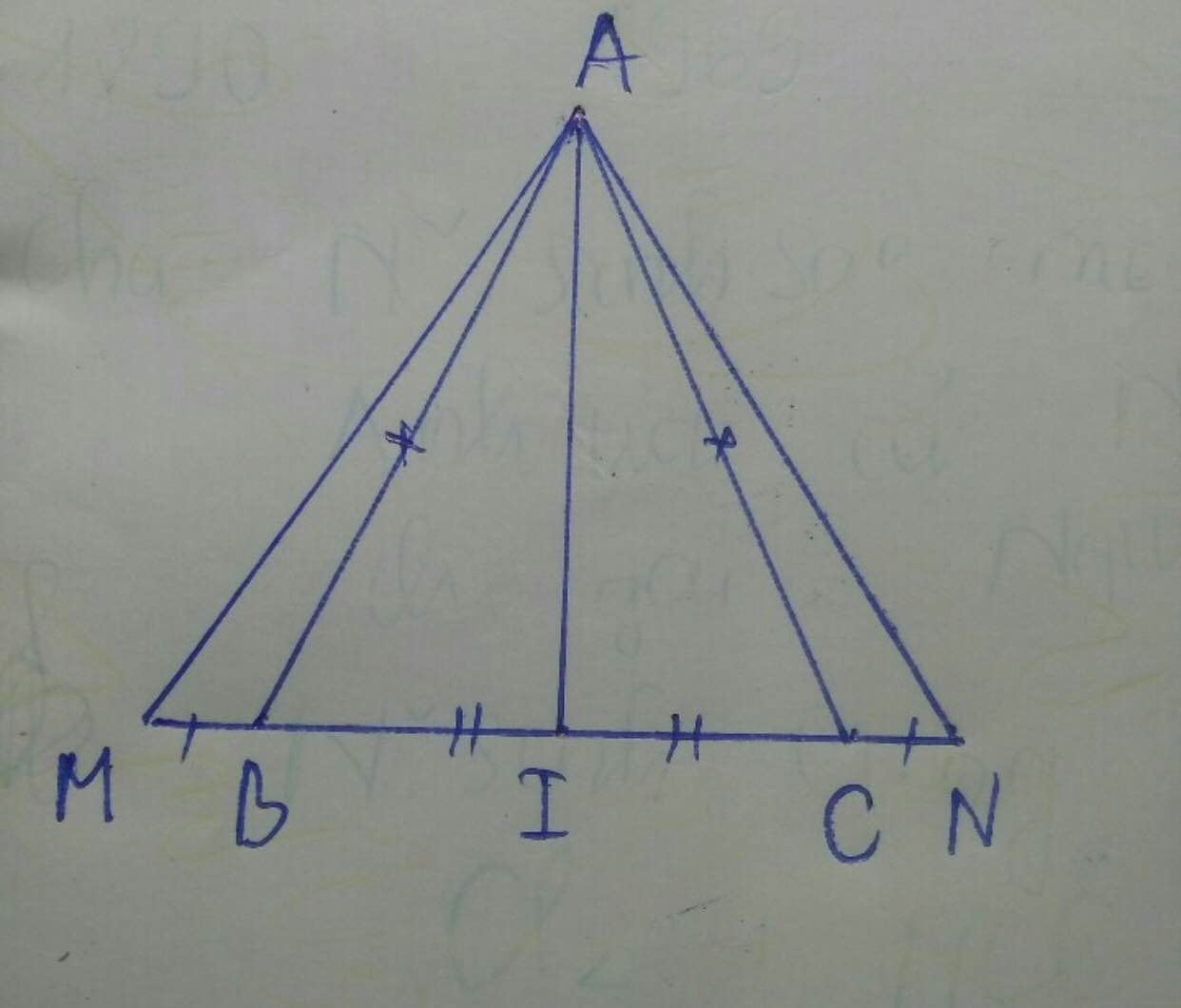
\(a,Xét.\Delta ABI=\Delta ACI:\\ AB=AC\\ AI.chung\\ BI=CI\\ \rightarrow\Delta.....=\Delta....\left(c.c.c\right)\\ \Rightarrow\widehat{BAI}=\widehat{CAI};\widehat{ABI}=\widehat{ACi}\\ \rightarrow AI.là.phâ.giác.của.\widehat{BAC}\\ b,\widehat{ABI}=\widehat{ACI}\left(chứng.minh.trên\right)\\ Ta.có:\)
\(\widehat{ABM}=180^0-\widehat{ABI}\\ \widehat{ACN}=180^0-\widehat{ACI} \\ \Rightarrow\widehat{ABM}=\widehat{ACN}\\ Xét.\Delta ABM.và.\Delta ACN.có:\\ AB=AC\\ \widehat{ABM}=\widehat{ACN}\\ BM=CN\\ \rightarrow\Delta...=\Delta...\left(c.g.c\right)\\ \Rightarrow AM=AN\)
\(c,Vì.\Delta ABI=\Delta ACI\\ \rightarrow\widehat{AIB}=\widehat{AIC}\\ Ta.có:\widehat{AIB}+\widehat{AIC}=180^0\\ \rightarrow\widehat{AIB}=\widehat{AIC}=\dfrac{180}{2}=90^0\\ \rightarrow AI\perp BC\)
Câu c sai đề mình sửa lại r đó:)