Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Gọi hệ số tỉ lệ của x và y là a, nghĩa là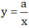 
hay x.y = a.
Ta có x = 4 thì y = 1,5 nên suy ra a = x.y = 4.1,5 = 6.
Vậy x.y = 6.
Khi x = 0,5 thì y = 6 : 0,5 = 12.
Khi x = -1,2 thì y = 6 : (-1,2) = -5
Khi y = 3 thì x = 6 : 3 =2
Khi y = -2 thì x = 6 : (-2) = -3.
Khi x = 6 thì y = 6 : 6 = 1.
Vậy ta có bảng sau :
| x | 0,5 | -1,2 | 2 | -3 | 4 | 6 |
| y | 12 | -5 | 3 | -2 | 1,5 | 1 |
Lời giải:
Vì $x,y$ là 2 đại lượng tỉ lệ nghịch nên tích của chúng không đổi. Theo giá trị trong bảng thì $xy=2(-6)=-12$ (đây chính là công thức mô tả mối quan hệ phụ thuộc của x,y.
Ta có bảng:
| x | 2 | 4 | 5 | -4 | -1,2 | -24 |
| y | -6 | -3 | -2,4 | 3 | 10 | 0,5 |
Có: x và y là 2 đại lượng tỉ lệ nghịch =>xy=a \(\left(a\ne0\right)\)
Vì x = 6 thì y = -4
=> a = 6.(-4)
=> a = -24
Vậy hệ số tỉ lệ giữa x và y là -24
Công thức liên hệ :
xy = -24
tao có
\(y=\frac{a}{x}\)hay \(xy=a\)
=> a = 6.(-4)=-24
vậy hệ số tỉ lệ là -24
công thức liên hệ
\(-4=\frac{-24}{6}\)
nhớ t.i.c.k
học tốt
Vì x và y là hai đại lượng tỉ lệ nghich nên xy = a (a ≠ 0)
Khi x = 2,5 thì y = -4 ⇒ a = 2,5.(-4) = -10
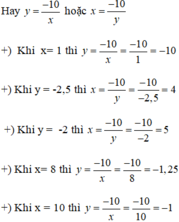
+ Từ đó ta có bảng sau:
| x | 1 | 2,5 | 4 | 5 | 8 | 10 |
| y | -10 | -4 | -2,5 | -2 | -1,25 | -1 |
Ta thấy: \(\dfrac{{0,5}}{{2,5}} = \dfrac{1}{5} = \dfrac{{1,5}}{{7,5}} = \dfrac{2}{{10}} = \dfrac{{2,5}}{{12,5}}\) nên x và y là 2 đại lượng tỉ lệ thuận.
Công thức liên hệ: \(x = \dfrac{1}{5}.y\) (hay y = 5.x)
`\color {blue} \text {_Namm_}`
`a,` Vì `y` tỉ lệ nghịch với `x` theo hệ số tỉ lệ `b -> y=b/x`
Thay `x=-3, y=6`
`-> 6=b/-3`
`-> b=-18`
Vậy, hệ số tỉ lệ `b=-18`
`b,` Khi `x=4 -> y=-18/4=-4,5`
`c,` Khi `-0,2 -> x= -18/-0,2=90`
a: k=xy=-18
=>y=-18/x
b: Khi x=4 thì y=-18/4=-9/2
c: khi y=-0,2 thì x=-18/y=-18/-0,2=90
a: xy=-24
nên x=-24/y
b: Hệ số tỉ lệ là k=-24
b: Khi y=12/5 thì x=-24:12/5=-24x5/12=-10
x | 2 | 4 | 5 | -4 | -1,2 | -24 |
y | -6 | -3 | -2,4 | 3 | 10 | 0,5 |
Vì x và y là hai đại lượng tỉ lệ nghịch, có x1y1 = 2.(-6) = -12 nên ta có công thức \(y = \dfrac{{ - 12}}{x}\).
Chúc bạn học tốt!
Từ cột thứ 2 ta tính được hệ số a từ công thức \(y=\frac{a}{x}.\)
=> \(a=\left(-15\right).\left(-4\right)=60.\) Từ đó tính được các số còn lại. Ta được bảng sau:
xy=60