Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1
\(x\) tỉ lệ thuận với y theo hệ số tỉ lệ là a nên \(x\) = ay
y tỉ lệ thuận với z theo hệ số tỉ lệ là b nên y = bz
Thay y = bz vào biểu thức \(x\) = ay ta có:
\(x\) = a.b.z
Vậy \(x\) tỉ lệ thuận với z theo hệ số tỉ lệ là a.b
Bài 2:
\(x\) tỉ lệ thuận với y theo hệ số tỉ lệ là m nên \(x\) = my
y tỉ lệ thuận với z theo hệ số tỉ lệ nghịch là n nên y = \(\dfrac{n}{z}\)
Thay y = \(\dfrac{n}{z}\) vào biểu thức \(x\) = m.y ta có:
\(x\) = m.\(\dfrac{n}{z}\)
\(x\) = \(\dfrac{m.n}{z}\)
Vậy \(x\) tỉ lệ nghịch với z theo hệ số tỉ lệ là m.n

Vì x tỉ lệ thuận với y theo hệ số tỉ lệ 2
\(\Rightarrow x=2y\) (1)
Vì y tỉ lệ nghịch với z theo hệ số tỉ lệ -3
\(\Rightarrow y\times z=-3\)
\(\Rightarrow y=-3:z\) (2)
Từ (1) và (2) \(\Rightarrow x=2.\left(-3\right):z\) \(\Rightarrow x=\frac{-6}{x}\)
Vậy x tỉ lệ nghịch với z theo hệ số tỉ lệ -6

Vì y tỉ lệ nghịch với x theo hệ số tỉ lệ a nên y = \(\dfrac{a}{x}\)
Vì x tỉ lệ nghịch với z theo hệ số tỉ lệ b nên x = \(\dfrac{b}{z}\)
Do đó, \(y = \dfrac{a}{x} = \dfrac{a}{{\dfrac{b}{z}}} = a:\dfrac{b}{z} = a.\dfrac{z}{b} = \dfrac{a}{b}.z\) ( \(\dfrac{a}{b}\) là hằng số vì a,b là các hằng số)
Vậy y có tỉ lệ thuận với z và hệ số tỉ lệ là \(\dfrac{a}{b}\).
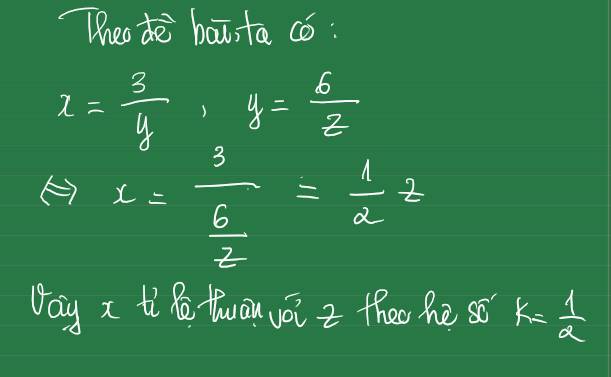
Lời giải:
Theo bài ra ta có:
$xy=\frac{1}{3}$
$yz=6$
$\Rightarrow \frac{xy}{yz}=\frac{1}{3}:6$
Hay $\frac{x}{z}=\frac{1}{18}$
$x=z.\frac{1}{18}$
Vậy $x$ tỉ lệ thuận với $z$ theo hệ số tỉ lệ $k=\frac{1}{18}$