Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

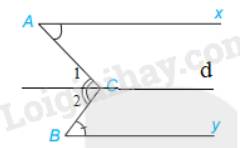
Qua C kẻ đường thẳng d song song với Ax
Vì Ax // By nên d // By
Vì d // Ax nên \(\widehat A = \widehat {{C_1}}\)(2 góc so le trong)
Vì d // By nên \(\widehat B = \widehat {{C_2}}\) (2 góc so le trong)
Mà \(\widehat C = \widehat {{C_1}} + \widehat {{C_2}}\)
Vậy \(\widehat C = \widehat A + \widehat B\)(đpcm)

Gọi By' là tia đối của tia By.
Gọi I là giao điểm của AC và yy'
By//Ax (gt) nên By'//Ax
Do By'//Ax nên xAC=AIy' ( so le trong)
Ta lại có: AIy=BIC ( đối đỉnh)
Do yBC là góc ngoài tại đỉnh B của tam giác BCI nên:
yBC=BIC+ACB
Mà xAC=AIy'
BIC=AIy'
=> xAC=BIC
Do đó yBC=xAC+ACB (đpcm)

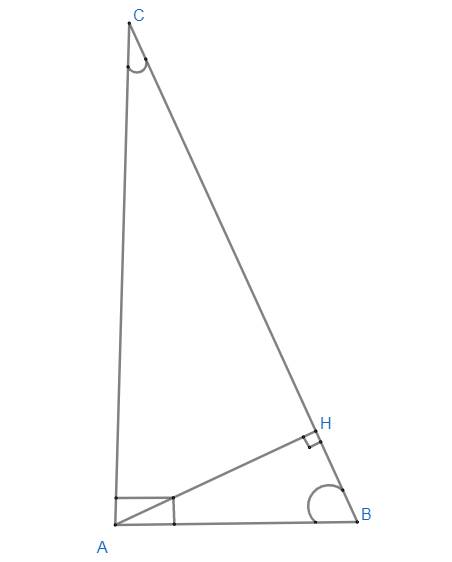
a)
Xét 2 tam giác vuông ABC và HAC có:
\(\widehat{C}\) chung
=> tg ABC \(\sim\) td HAC (g.g)
=> \(\widehat{ABC}=\widehat{HAC}\)
b)
Xét 2 tg vuông ACB và HAB có:
\(\widehat{B}\) chung
=> tg ACB \(\sim\) tg HAB (g.g)
=> \(\widehat{ACB}=\widehat{HAB}\)

Bạn xem có phải hình vẽ thế này ko nhá!
a, \(\widehat{NAC}=\widehat{ACB}\Rightarrow\)AN//BC (2 góc so le trong bằng nhau)
\(\Rightarrow\widehat{MAB}=\widehat{ABC}\) (2 góc so le trong)
b, Do NA//BC suy ra NM//BC suy ra
\(\widehat{MAx}=\widehat{ACB}=55^o\) (2 góc đồng vị)
c, DO \(\widehat{MAx}=\widehat{ACB}\) và \(\widehat{MAB}=\widehat{ABC}\)(chứng minh trên)
Mặt khác \(\widehat{ABC}=\widehat{ACB}\left(\widehat{B}=\widehat{C}\right)\)(giả thiết)
suy ra \(\widehat{MAx}=\widehat{MAB}\)suy ra MA là tia phân giác của \(\widehat{BAx}\)

nhanh lên mình cần gấp lắm
giúp mình với huhuhuhuhuhuhuhuhuhuhuhuhuhuhuhuhuhu