Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo:

Dễ thấy: \(\overrightarrow {OA} = \overrightarrow {OM} + \overrightarrow {MA} \); \(\overrightarrow {OB} = \overrightarrow {OM} + \overrightarrow {MB} \)
Tương tự: \(\overrightarrow {OC} = \overrightarrow {ON} + \overrightarrow {NC} \); \(\overrightarrow {OD} = \overrightarrow {ON} + \overrightarrow {ND} \)
\(\begin{array}{l} \Rightarrow \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \left( {\overrightarrow {OM} + \overrightarrow {MA} } \right) + \left( {\overrightarrow {OM} + \overrightarrow {MB} } \right) + \left( {\overrightarrow {ON} + \overrightarrow {NC} } \right) + \left( {\overrightarrow {ON} + \overrightarrow {ND} } \right)\\ = \left( {\overrightarrow {OM} + \overrightarrow {OM} + \overrightarrow {MA} + \overrightarrow {MB} } \right) + \left( {\overrightarrow {ON} + \overrightarrow {ON} + \overrightarrow {NC} + \overrightarrow {ND} } \right)\\ = \overrightarrow {OM} + \overrightarrow {OM} + \overrightarrow {ON} + \overrightarrow {ON} \\ = \left( {\overrightarrow {OM} + \overrightarrow {ON} } \right) + \left( {\overrightarrow {OM} + \overrightarrow {ON} } \right)\\ = \overrightarrow 0 + \overrightarrow 0 \\ = \overrightarrow 0 .\end{array}\)

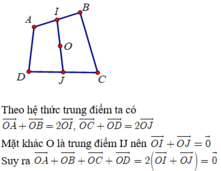
\(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=2\cdot\left(\overrightarrow{OE}+\overrightarrow{OF}\right)=\overrightarrow{0}\)

\(\overrightarrow{BM}+\overrightarrow{CN}+\overrightarrow{AP}\)
\(=\dfrac{1}{2}\left(\overrightarrow{BC}+\overrightarrow{CA}+\overrightarrow{AP}\right)\)
\(=\overrightarrow{0}\)

\(\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AB}+\overrightarrow{CB}+\overrightarrow{BD}=\overrightarrow{AB}+\overrightarrow{BD}+\overrightarrow{CB}=\overrightarrow{AD}+\overrightarrow{CB}\)
\(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=\left(\overrightarrow{OE}+\overrightarrow{EA}\right)+\left(\overrightarrow{OF}+\overrightarrow{FB}\right)+\left(\overrightarrow{OE}+\overrightarrow{EC}\right)+\left(\overrightarrow{OF}+\overrightarrow{FD}\right)\)
\(=2\left(\overrightarrow{OE}+\overrightarrow{EF}\right)+\left(\overrightarrow{EA}+\overrightarrow{EC}\right)+\left(\overrightarrow{FB}+\overrightarrow{FD}\right)\)
\(=2.\overrightarrow{0}+\overrightarrow{0}+\overrightarrow{0}=\overrightarrow{0}\)

Do M là trung điểm BC nên: \(\overrightarrow{AM}=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\)
Tương tự: \(\overrightarrow{BN}=\dfrac{1}{2}\overrightarrow{BA}+\dfrac{1}{2}\overrightarrow{BC}\) ; \(\overrightarrow{CP}=\dfrac{1}{2}\overrightarrow{CA}+\dfrac{1}{2}\overrightarrow{CB}\)
Cộng vế:
\(\overrightarrow{AM}+\overrightarrow{BN}+\overrightarrow{CP}=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{BA}+\dfrac{1}{2}\overrightarrow{BC}+\dfrac{1}{2}\overrightarrow{CA}+\dfrac{1}{2}\overrightarrow{CB}\)
\(=\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{BA}\right)+\dfrac{1}{2}\left(\overrightarrow{AC}+\overrightarrow{CA}\right)+\dfrac{1}{2}\left(\overrightarrow{BC}+\overrightarrow{CB}\right)=\overrightarrow{0}\)
b. Từ câu a ta có:
\(\overrightarrow{AM}+\overrightarrow{BN}+\overrightarrow{CP}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{AO}+\overrightarrow{OM}+\overrightarrow{BO}+\overrightarrow{ON}+\overrightarrow{CO}+\overrightarrow{OP}=\overrightarrow{0}\)
\(\Leftrightarrow-\overrightarrow{OA}+\overrightarrow{OM}-\overrightarrow{OB}+\overrightarrow{ON}-\overrightarrow{OC}+\overrightarrow{OP}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{OM}+\overrightarrow{ON}+\overrightarrow{OP}\) (đpcm)

câu 2 ( các kí hiệu vecto khi lm bài thỳ b tự viết nhé mk k viết kí hiệu để trả lời cho nhanh hỳ hỳ )
OA+ OB + OC = OA'+ OB' + OC'
<=> OA - OA' + OB - OB' + OC - OC' = 0
<=> A'A + B'B + C'C = 0
<=> 2 ( BA + CB + AC ) = 0
<=> 2 ( CB + BA + AC ) = 0
<=> 2 ( CA + AC ) = 0
<=> 0 = 0 ( luôn đúng )
câu 1 ( các kí hiệu vecto b cx tự viết nhá )
VT = OD + OC = OA + AD + OB + BC = OA + OB + AD + BC = BO + OB + AD + BC = 0 + AD + BC = AD + BC = VP ( đpcm)