Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
Góc A + Góc B + góc C + góc D = 3600 (toonge 4 góc trong tứ giác)
Mà góc C = 800 và góc D = 700 nên góc A + góc B = 2100
Theo đề bài, thì AI và BI lần lượt là tia phân giác của góc A và góc B nên góc IAB + góc IBA = 2100 : 2 = 105 độ.
Xét tam giác IAB ta có: góc AIB = 180 độ - 105 độ = 75 độ.
Vậy góc AIB = 75 độ.
A B C D 80* 70*
Ta có: \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\) (tổng 4 góc trong tứ giác)
Mà: \(\widehat{C}=80^o\text{ và }\widehat{D}=70^o\text{ nên }\widehat{A}+\widehat{B}=210^o\)
Theo đề bài, Thì AI và BI lần lượt là tia phân giác của \(\widehat{A}\) và \(\widehat{B}\) nên \(\widehat{IAB}+\widehat{IBA}=\frac{210^o}{2}=150^o\)
Xét \(\Delta IAB,\text{ ta có: }\widehat{AIB}=180^o-150^o=75^o\)
\(\Rightarrow\widehat{AIB}=75^o\)

A B C O E H Y F
câu a
có OE vuông góc với bc =>tam giác OEC vuông tại E
có OH vuông góc với AC => tam giác OHC vuông tại H
xét tam giác vuông OEC và tam giác vuông OHC
có : góc ECO = góc HCO( OC là phân giác của góc C )
OC là cạnh chung
=> tam giác vuông ECO = tam giác vuông HCO ( trườnghợp đặc biệt của tam giác vuông : cạnh huyền - góc nhọn )
câu b
có tam giác vuông OEC = tam giác vuông HCO (chứng minh ở câu a )
=> EC = HC ( 2 cạnh tương ứng )
xét tam giác ECY và tam giác YCH
có : EC = EH( chứng minh trên )
góc ECY= góc YCH (phan giác góc C )
CY cạnh chung
=> tam giác ECY = tam giác YCH (trường hợp : c-g-c)
=> EY = YH ( 2 cạnh tương ứng ) => Y là trungđiểm của EH (1)
=> góc EYC = góc HYC ( 2 góc tương ứng )
Mà góc EYC + góc HYC = 180 độ ( 2 góc kề bù )
mà góc EYC = góc HYC (chứng minh trên ) => góc EYC =góc HYC = 900 => CY vuông với EH tại Y hay CO cũng vuông góc với EH (2)
từ (1) và (2) => OC làđường trung trực của HE
câu c
có tam giác vuông OEC = tam giác vuông OHC (chứng minh ở câu a )
=> OE = OH( 2 cạnh tương ứng )
có OFvuông góc với AB => tam giác BFO vuông tại F
có OE vuông góc với BC => tam giác OBE vuông tại E
xét tam giác vuông BFO và tam giác vuông BEO
có :góc FBO = góc EBO( fân giác của góc B)
Bo là cạnh chung
=> tam giác vuông FBO =tam giác vuông EBO ( trường hợp đặt biệt của tam giác cuông : cạnh huyền - góc nhọn)
=> OF= OE ( 2 cạnh tương ứng )
mà OE=OH
=> OF = OH => điều phải chứng minh (câu c ý 1 )
câu c ý 2 :
xét tam giá vuông OFA và tamgiác vuông OHA
có:FO=OH ( chứng minh trên)
OA là cạnh chung
=>tam giác vuông FOA = tam giác vuông OHA ( trường hợp đặc biệt của tam giác vuông : cạnh huyền - cạnh góc vuông )
=> góc AOF = góc AOH ( 2 góc tương ứng )
câu d
lát làm nha ,giờ mk có việc r,có j ib mk mk làm nốt ,

Dễ cậu tk mk trước rồi mk trả lời mk học lớp 8 rùi nhóm chọn toán lun đó
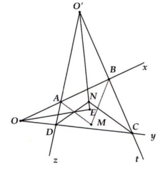

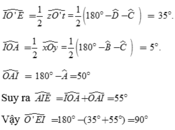
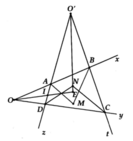
a: Gọi giao điểm của hai tia phân giác của hai góc BAD;ADC là M
Theo đề, ta có: MA\(\perp\)MD
=>ΔMAD vuông tại M
ΔMAD vuông tại M
=>\(\widehat{MAD}+\widehat{MDA}=90^0\)
=>\(\dfrac{1}{2}\left(\widehat{BAD}+\widehat{ADC}\right)=90^0\)
=>\(\widehat{BAD}+\widehat{ADC}=180^0\)
mà hai góc này là hai góc ở vị trí trong cùng phía
nên AB//CD
=>ABCD là hình thang
b: Sửa đề: Hai tia phân giác của góc C và góc B cũng vuông góc với nhau
Gọi N là giao điểm của hai tia phân giác của hai góc ABC và góc BCD
AB//CD
=>\(\widehat{ABC}+\widehat{BCD}=180^0\)(hai góc trong cùng phía)
=>\(2\cdot\left(\widehat{NBC}+\widehat{NCB}\right)=180^0\)
=>\(\widehat{NBC}+\widehat{NCB}=90^0\)
=>ΔNBC vuông tại N
=>NB vuông góc NC(ĐPCM)