Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1/nối AC
Do AB//CD=>BAC=ACD(so le trong)
Do AD//BC=>ACB=DAC(so le trong)
Xét ∆ABC và ∆ACD
ACB=DAC(chứng minh trên)
BAC=DAC(chứng minh trên)
AC chung
Vậy ∆ABC=∆CDA(g.c.g)=>AB=DC(cặp cạnh tương ứng)
AD=BC(cặp cạnh tương ứng)

Chứng minh rằng AK=KC,BI=ID
vì FE là đường trung bình hình thang nên FE//AB//CD
E, F là trung điểm của AD và BC nên AK=KC
BI=ID
( trong tam giác đường thẳng qua trung điểm của 1 cạnh, // với cạnh thứ 2 thì qua trung điểm cạnh thứ 3)
Xét t/g ABC và t/g CDA có :
AC cạnh chung
AB = CD ( gt )
\(\widehat{A1}=\widehat{C1}\)( slt , AB // CD )
\(\Rightarrow\)t/g ABC = t/g CDA ( c-g-c )
\(\Rightarrow\)BC = AD
\(\widehat{A2}=\widehat{C2}\) và 2 góc này ở vị trí slt
\(\Rightarrow\)BC // AD

b: Xét tứ giác ABCD có
AB=CD
AD=BC
Do đó: ABCD là hình bình hành
Suy ra: AB//CD;AD//BC

a.Cho tứ giác ABCD biết AB//CD và AB=CD.CMR AD//BC và AD=BC
A B C D
Ta có :\(\left\{{}\begin{matrix}\text{AB // CD}\\AB=CD\end{matrix}\right.\)(gt)
=> Tứ giác ABCD là hình bình hành
=> \(\left\{{}\begin{matrix}\text{AD //BC}\\AD=AD\end{matrix}\right.\)(tính chất hình bình hành)
b.Cho tứ giác ABCD biết AB//CD và AD//BC.CMR:AB=CD và AD=BC
ABCD
Ta có : \(\left\{{}\begin{matrix}\text{AB //CD}\\\text{AD //BC}\end{matrix}\right.\) (gt)
=> Tứ giác ABCD là hình bình hành
Do đó : \(\left\{{}\begin{matrix}AB=CD\\AD=BC\end{matrix}\right.\)(tính chất hình bình hành)
c.Cho tứ giác ABCD biết AB=CD và AD=BC.CMR AD//BC và AD//BC
ABCD
Ta có : \(\left\{{}\begin{matrix}AB=CD\\AD=BC\end{matrix}\right.\) (gt)
=> Tứ giác ABCD là hình bình hành
=> AD //BC (tính chất hình bình hành)
*Bạn cũng có thể xét các tứ giác là hình vuông, hình chữ nhật cũng có tính chất tương tự.
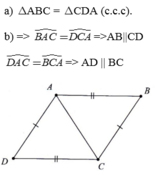
Hình minh họa A B D C 1 2 1 2 Nối A với C
Chứng minh:
Vì AD // BC \(\Rightarrow\widehat{A2}=\widehat{C2}\left(slt\right)\)
Vì AB // CD \(\Rightarrow\widehat{A1}=\widehat{C1}\left(slt\right)\)
Xét △CAD và △ACB có:
\(\widehat{A2}=\widehat{C2}\left(cmt\right)\)
AC - cạnh chung
\(\widehat{A1}=\widehat{C1}\left(cmt\right)\)
⇒ △CAD = △ACB( g.c.g )
⇒ CD = AB ( tương ứng )
⇒ AD = CB ( tương ứng )