Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a)
Do \(\overrightarrow{AB}=\overrightarrow{DC}\) nên AB // DC và AB = DC .
Vì vậy tứ giác ABCD là là hình bình hành.
Từ đó suy ra: AD = BC và AD//BC nên \(\overrightarrow{AD}=\overrightarrow{BC}\).
Cách 2:
Áp dụng quy tắc ba điểm ta có:
\(\overrightarrow{AB}=\overrightarrow{DC}\Leftrightarrow\overrightarrow{AD}+\overrightarrow{DB}=\overrightarrow{DB}+\overrightarrow{BC}\)\(\Leftrightarrow\overrightarrow{AD}=\overrightarrow{BC}\).
Tứ giác ABCD là hình bình hành
\( \Leftrightarrow \left\{ \begin{array}{l}
AB // DC\\
AB = DC
\end{array} \right.\)
Mà \(AB // DC \Leftrightarrow \overrightarrow {AB} ,\, \overrightarrow {DC} \) cùng phương, do đó cùng hướng.
\( \Leftrightarrow \left\{ \begin{array}{l}
\overrightarrow {AB} , \overrightarrow {DC} \,{\rm{ cùng hướng}}\\
AB = DC
\end{array} \right.\)
\(\Leftrightarrow \overrightarrow {AB} = \overrightarrow {DC} \)
Vậy tứ giác ABCD là hình bình hành khi và chỉ khi \(\overrightarrow {AB} = \overrightarrow {DC} \).
Ta có:
\(\overrightarrow {MN} = \overrightarrow {MA} + \overrightarrow {AD} + \overrightarrow {DN} \)
Mặt khác: \(\overrightarrow {MN} = \overrightarrow {MB} + \overrightarrow {BC} + \overrightarrow {CN} \)
\(\begin{array}{l} \Rightarrow 2\overrightarrow {MN} = \overrightarrow {MA} + \overrightarrow {AD} + \overrightarrow {DN} + \overrightarrow {MB} + \overrightarrow {BC} + \overrightarrow {CN} \\ \Leftrightarrow 2\overrightarrow {MN} = \left( {\overrightarrow {MA} + \overrightarrow {MB} } \right) + \left( {\overrightarrow {DN} + \overrightarrow {CN} } \right) + \overrightarrow {BC} + \overrightarrow {AD} \\ \Leftrightarrow 2\overrightarrow {MN} = \overrightarrow 0 + \overrightarrow 0 + \overrightarrow {BC} + \overrightarrow {AD} \\ \Leftrightarrow 2\overrightarrow {MN} = \overrightarrow {BC} + \overrightarrow {AD} \end{array}\)
Lại có:
\(\overrightarrow {BC} + \overrightarrow {AD} = \overrightarrow {BD} + \overrightarrow {DC} + \overrightarrow {AD} = \overrightarrow {AD} + \overrightarrow {DC} + \overrightarrow {BD} = \overrightarrow {AC} + \overrightarrow {BD} .\)
Vậy \(\overrightarrow {BC} + \overrightarrow {AD} = 2\overrightarrow {MN} = \;\overrightarrow {AC} + \overrightarrow {BD} .\)
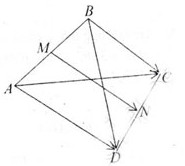
N là trung điểm của CD:
2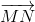
=
+ 
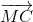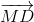(1)
Theo quy tắc 3 điểm, ta có:
= 
+
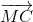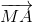(2)
= 
+ 
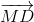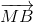(3)
Từ (1), (2), (3) ta có: 2= +++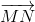
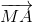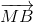
vì M là trung điểm của Ab nên: + =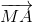 
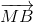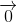
Suy ra : 2 = +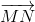
Chứng minh tương tự, ta có 2 =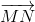 
+
Chú ý: Sau khi chứng minh 2 C = + ta chỉ cần chứng minh thêm + = + cũng được
Ta có: + = 
++
+
= +++= ++
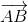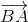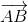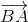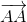
Vì 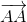= 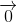nên ta có: +=+
và 2= + = +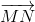
Tứ giác ABCD là một hình bình hành \( \Leftrightarrow \left\{ \begin{array}{l}AD//\;BC\\AD = BC\end{array} \right.\)
\( \Leftrightarrow \) Hai vecto \(\overrightarrow {AD} \) và \(\overrightarrow {BC} \) cùng hướng và AD = BC.
\( \Leftrightarrow \overrightarrow {BC} = \overrightarrow {AD} .\) (đpcm)
Ta chứng minh hai mệnh đề:
- Khi =
thì ABCD là hình bình hành.
Thật vậy, theo định nghĩa của vec tơ bằng nhau thì:
=
⇔
=
và và
cùng hướng.
và
cùng hướng =>
và
cùng phương, suy ra giá của chúng song song với nhau, hay AB // DC (1)
Ta lại có =
=> AB = DC (2)
Từ (1) và (2), theo dấu hiệu nhận biết hình bình hành, tứ giác ABCD có một cặp cạnh song song và bằng nhau nên nó là hình bình hành.
- Khi ABCD là hình bình hành thì =
Khi ABCD là hình bình hành thì AB // CD. Dễ thấy, từ đây ta suy ra hai vec tơ và
cùng hướng (3)
Mặt khác AB = CD => =
(4)
Từ (3) và (4) suy ra =
.
a) \(\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} + \overrightarrow {DA} = \left( {\overrightarrow {AB} + \overrightarrow {BC} } \right) + \left( {\overrightarrow {CD} + \overrightarrow {DA} } \right) = \overrightarrow {AC} + \overrightarrow {CA} = \overrightarrow {AA} = \overrightarrow 0 \)
b) \(\overrightarrow {AB} - \overrightarrow {AD} = \overrightarrow {AB} + \overrightarrow {DA} = \overrightarrow {DA} + \overrightarrow {AB} = \overrightarrow {DB} \)
c) \(\overrightarrow {CB} - \overrightarrow {CD} = \overrightarrow {CB} + \overrightarrow {DC} = \overrightarrow {DC} + \overrightarrow {CB} = \overrightarrow {DB} \)
\(\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AB}+\overrightarrow{CB}+\overrightarrow{BD}=\overrightarrow{AB}+\overrightarrow{BD}+\overrightarrow{CB}=\overrightarrow{AD}+\overrightarrow{CB}\)
\(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=\left(\overrightarrow{OE}+\overrightarrow{EA}\right)+\left(\overrightarrow{OF}+\overrightarrow{FB}\right)+\left(\overrightarrow{OE}+\overrightarrow{EC}\right)+\left(\overrightarrow{OF}+\overrightarrow{FD}\right)\)
\(=2\left(\overrightarrow{OE}+\overrightarrow{EF}\right)+\left(\overrightarrow{EA}+\overrightarrow{EC}\right)+\left(\overrightarrow{FB}+\overrightarrow{FD}\right)\)
\(=2.\overrightarrow{0}+\overrightarrow{0}+\overrightarrow{0}=\overrightarrow{0}\)
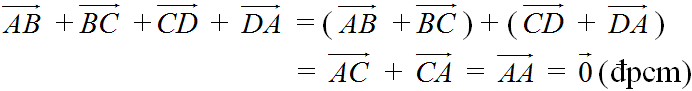
\(\overrightarrow{AD}=\overrightarrow{AB}+\overrightarrow{BD}\)
\(\overrightarrow{BC}=\overrightarrow{BD}+\overrightarrow{DC}\)
Mà \(\overrightarrow{AB}=\overrightarrow{DC}\) (gt)
\(\Rightarrow\overrightarrow{AD}=\overrightarrow{BC}\)