Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D

Từ giả thiết ta thấy ![]() và OBC là tam giác vuông nên thể tích cần tìm là:
và OBC là tam giác vuông nên thể tích cần tìm là:
VO.ABC = 1 3 OA.SOBC = 1 6 OA.OB.OC = abc 6

Chọn D

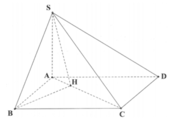
Từ giả thiết suy ra: ΔABC cân tại A có:

Gọi I là trung điểm của BC ⇒ A I ⊥ B C
Giả sử H là trực tâm của tam giác ABC.
Ta thấy O A ⊥ O B C
Vì O B ⊥ O A C ⇒ O B ⊥ A C và A C ⊥ B H nên A C ⊥ O B H ⇒ O H ⊥ A C ( 1 )
B C ⊥ O A I ⇒ O H ⊥ B C ( 2 )
Từ (1) và (2) suy ra O H ⊥ A B C
Có O I = 1 2 B C = a 2 2 = O A
=> ΔAOI vuông cân tại O => H là trung điểm AI và O H = 1 2 A I = a 2
Khi đó:

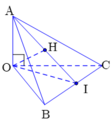
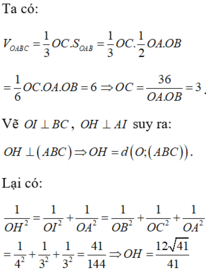
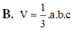
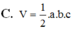
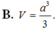
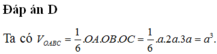

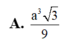
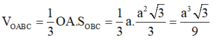
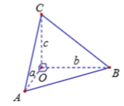
Trong tam giác OBC, kẻ đường cao OH \(\Rightarrow BC\perp\left(AOH\right)\)
\(\frac{1}{OH^2}=\frac{1}{OB^2}+\frac{1}{OC^2}\Rightarrow OH=\frac{OB.OC}{\sqrt{OB^2+OC^2}}=\frac{6a}{\sqrt{13}}\)
Trong tam giác vuông AOH, từ O kẻ \(OK\perp AH\Rightarrow OK\perp\left(ABC\right)\)
\(\frac{1}{OK^2}=\frac{1}{OH^2}+\frac{1}{OA^2}\Rightarrow OK=\frac{OA.OH}{\sqrt{OA^2+OH^2}}=\frac{3a\sqrt{14}}{7}\)