Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

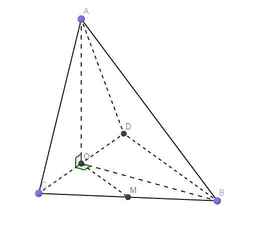
Đặt \(OA=OB=2OC=2a\)
\(\Rightarrow BC=\sqrt{OB^2+OC^2}=a\sqrt{5}\) \(\Rightarrow OM=\dfrac{1}{2}BC=\dfrac{a\sqrt{5}}{2}\)
Qua B kẻ đường thẳng song song OM cắt OC kéo dài tại D
\(\Rightarrow OM\) là đường trung bình tam giác BCD \(\Rightarrow BD=2OM=a\sqrt{5}\)
\(OM||BD\Rightarrow\left(OM;AB\right)=\left(BD;AB\right)=\widehat{ABD}\)
\(AB=\sqrt{OA^2+OB^2}=2a\sqrt{2}\)
\(AD=\sqrt{OA^2+OD^2}=\sqrt{OA^2+OC^2}=a\sqrt{5}\)
\(\Rightarrow cos\widehat{ABD}=\dfrac{AB^2+BD^2-AD^2}{2AB.BD}=\dfrac{\sqrt{10}}{5}\)

Cau 33:
\(\left|\overrightarrow{u}-\overrightarrow{v}\right|=\sqrt{\left(\overrightarrow{u}-\overrightarrow{v}\right)^2}=\sqrt{u^2+v^2-2\cdot u\cdot v\cdot cos120}\)
\(=\sqrt{4^2+3^2-2\cdot4\cdot3\cdot\dfrac{-1}{2}}=\sqrt{37}\)

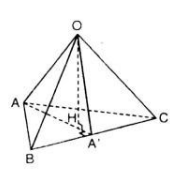
Chúng ta biết rằng tứ diện OABC có ba cạnh OA, OB, OC đôi một vuông góc với nhau. Vì vậy, ta có thể xem tứ diện OABC là một hình chữ nhật với cạnh OA, OB, OC.
Gọi SABC là diện tích của hình chữ nhật OABC. Ta có:
SABC = OA x OB
Gọi SHBC là diện tích của tam giác HBC. Ta có:
SHBC = 1/2 x HB x BC
Vì tứ diện OABC là một hình chữ nhật, nên ta có:
SOAB = OA x OB
Vậy, ta có:
(SOAB)2 = (OA x OB)2
= OA2 x OB2
= SABC x SHBC
= SABC + SHBC
Vậy, ta đã chứng minh được rằng (SOAB)2 = SABC + SHBC.