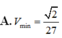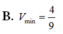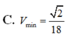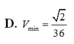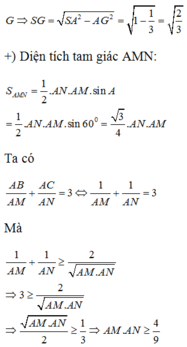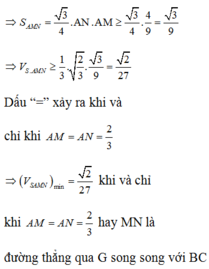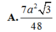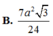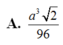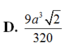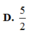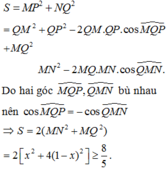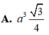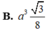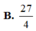Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
Vì tam giác SAC vuông tại A
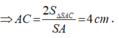
![]()
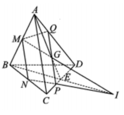
nên tam giác ABC vuông tại A. Chọn hệ trục Oxyz như hình vẽ
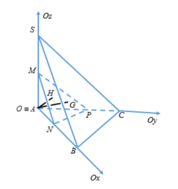
Ta có
A(0;0;0), B(3;0;0), C(0;4;0), S(0;0;3)
Vì G là trọng tâm của tứ diện SABC nên ta có
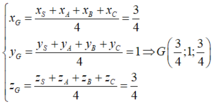
Gọi H là hình chiếu của điểm A lên mặt phẳng α . Theo tính chất của tam diện vuông ta có
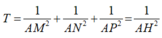
![]()
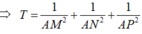
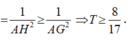
Dấu “=” xảy ra khi H ≡ G tức mặt phẳng α đi qua điểm G và vuông góc với đường thẳng OG.
Vậy giá trị nhỏ nhất của T bằng 8 17

Ta tính thể tích hình chóp A’.BCB’. Gọi M là trung điểm của B’C’, ta có: ATM ⊥ B’C’ (1)
Lăng trụ ABC.A’B’C’ là lăng trụ đứng nên: BB’ ⊥ (A’B’C’) ⇒BB’⊥ A’M (2)
Từ (1) và (2) suy ra
AM⊥ (BB’C) hay A’M là đường cao của hình chóp A’.BCB’


Chọn A
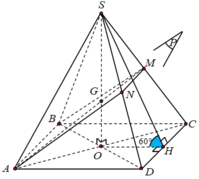
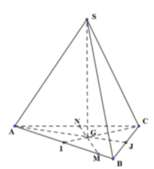
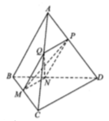
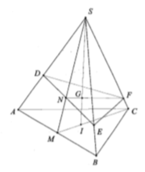
Gọi H là trung điểm cạnh CD và O là tâm hình vuông ABCD.
Ta có S. ABCD là hình chóp tứ giác đều nên các mặt bên hợp với đáy các góc bằng nhau
Giả sử S C D , A B C D ^ = S H O ^ = 60 o
Tam giác SHO vuông tại O có:
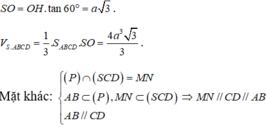
Mà G là trọng tâm tam giác SAC nên G cũng là trọng tâm tam giác SBD
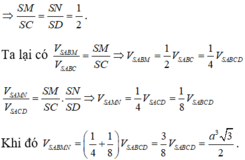

Chọn D.
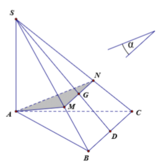
Do ( α ) đi qua G ∈ (SBC), song song với BC nên ( α ) cắt mặt phẳng (SBC) theo giao tuyến MN qua G và song song với BC.
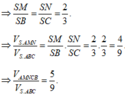
Do tam giác ABC vuông cân tại B, AC = a
2
nên ![]()
Do SA
⊥
(ABC) nên ![]()
![]()