Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu hỏi của Julian Edward - Toán lớp 11 | Học trực tuyến

a) △ABC có M và N là trung điểm của AB, BC nên MN // AC (1)
△ACD có P và Q là trung điểm của CD, DA nên PQ // AC (2)
△SMN có I và J là trung điểm của SM, SN nên IJ // MN (3)
△SPQ có L và K là trung điểm của SQ, SP nên LK // PQ (4)
Từ (1)(2)(3)(4) suy ra IJ // LK. Do đó: I, J, K, L đồng phẳng.
Ta có: \(\dfrac{MN}{AC}=\dfrac{QP}{AC}=\dfrac{1}{2}\)
\(\dfrac{IJ}{MN}=\dfrac{LK}{PQ}=\dfrac{1}{2}\)
Từ (6)(7) suy ra: IJ = LK mà IJ // LK
Do đó: IJKL là hình bình hành.
b) Ta có: M, P lần lượt là trung điểm của AB, CD
Suy ra: MP // BC (1)
△SMP có: I, K là trung điểm của SM, SP
Suy ra: IK // MP (2)
Từ (1)(2) suy ra: IK // BC.
c) Ta có: J là điểm chung của hai mặt phẳng (IJKL) và (SBC)
Mà: IK // BC
Từ J kẻ Jx sao cho Jx // BC. Do đó, Jx là giao tuyến của hai mặt phẳng (IJKL) và (SBC).

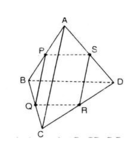
a) Ta có:
PQ = (ABC) ∩ (PQRS)
RS = (PQRS) ∩ (ACD)
AC = (ABC) ∩ (ACD)
Vậy hoặc PQ, RS, AC đồng qui hoặc song song.
b) PS =(ABD) ∩ (PQRS)
RQ = (BCD) ∩ (PQRS)
BD = (ABD) ∩ (CBD)
Vậy PS, RQ, BD đồng quy hoặc song song.
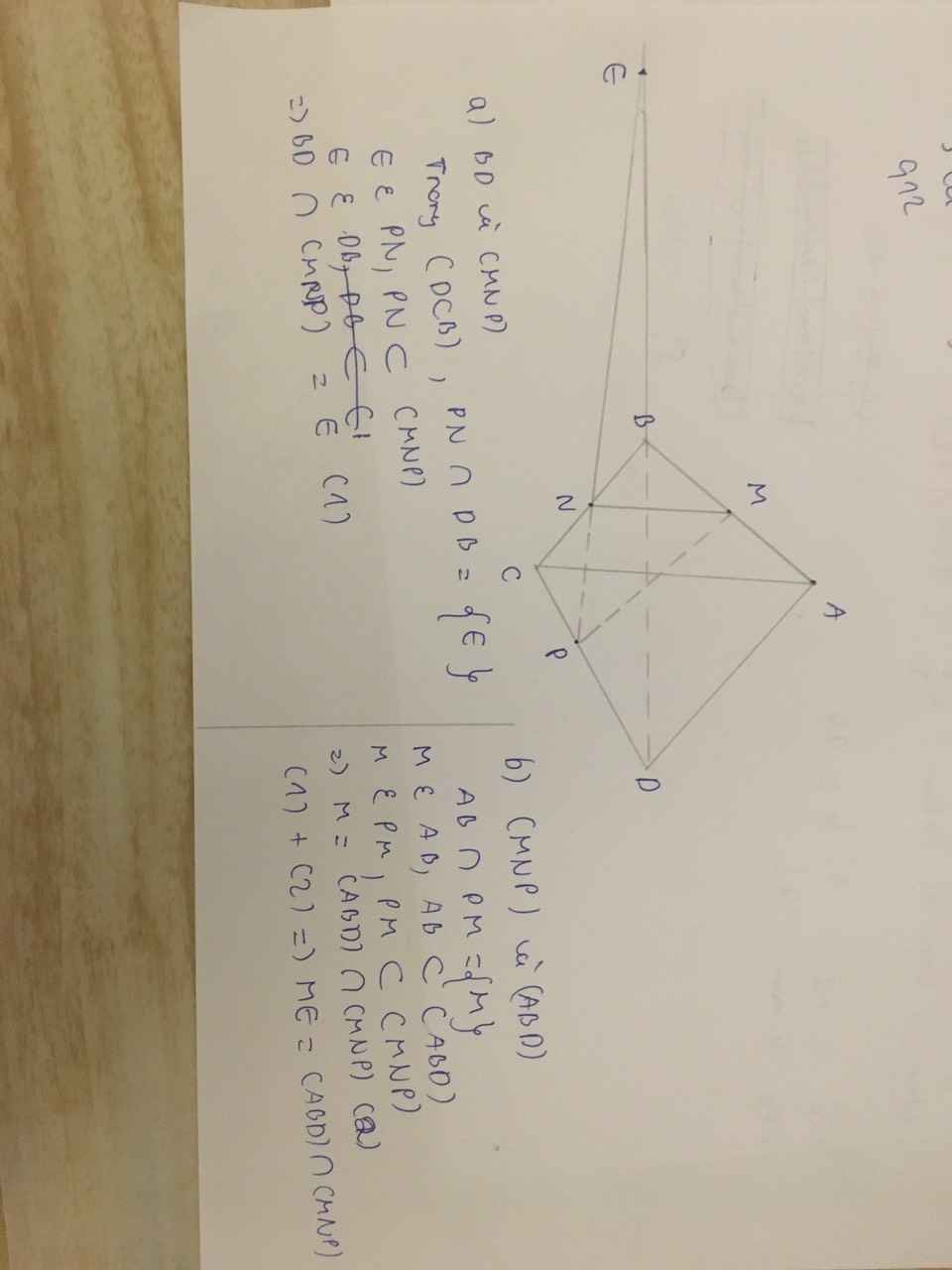
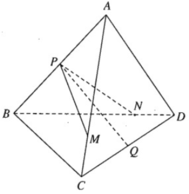
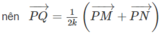
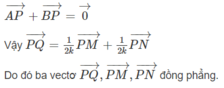


Nối NP kéo dài cắt BD tại E
Áp dụng định lý Menelaus cho tam giác CBD:
\(\frac{NC}{NB}.\frac{BE}{ED}.\frac{DP}{PC}=1\Leftrightarrow3.\frac{BE}{ED}.2=1\Rightarrow\frac{BE}{ED}=\frac{1}{6}\Rightarrow\frac{DE}{EB}=6\)
Trong mặt phẳng (ABD), nối EM kéo dài cắt AD tại Q
Áp dụng định lý Menelaus cho tam giác ABD:
\(\frac{QA}{QD}.\frac{DE}{EB}.\frac{BM}{MA}=1\Leftrightarrow\frac{QA}{QD}.6.\frac{3}{2}=1\Leftrightarrow QD=9QA\)
\(\Rightarrow k=9\)