Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

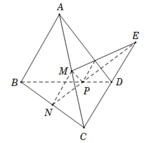
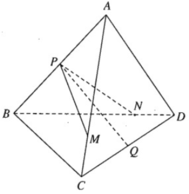
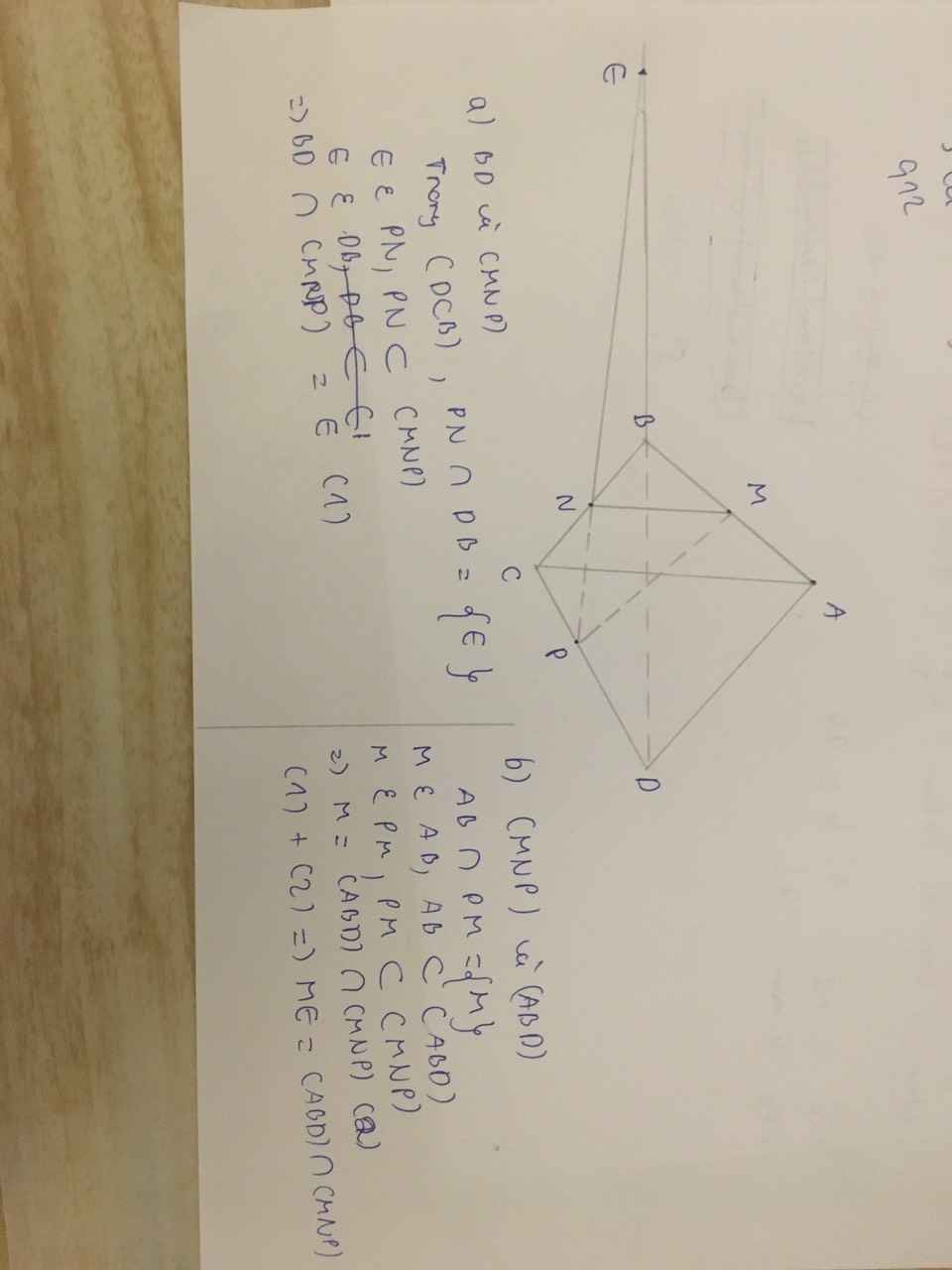
Chọn mặt phẳng phụ chứa CD là (BCD)
Do NP không song song CD nên NP cắt CD tại E
Điểm E ∈ N P ⇒ E ∈ M N P .
Vậy C D ∩ M N P tại E.
Chọn A

Trong mp (ACD) kéo dài MN và CD cắt nhau tại I
Trong mp (BCD) nối IQ cắt BD tại J
Áp dụng định lý Menelaus trong tam giác ACD:
\(\dfrac{AM}{MC}.\dfrac{CI}{ID}.\dfrac{DN}{NA}=1\Rightarrow1.\dfrac{CI}{ID}.\dfrac{1}{2}=1\Rightarrow IC=2ID\)
Do \(BC=4BQ\Rightarrow QC+QB=4QB\Rightarrow QC=3QB\)
Menelaus cho tam giác BCD:
\(\dfrac{QC}{QB}.\dfrac{BJ}{JD}.\dfrac{DI}{IC}=1\Rightarrow3.\dfrac{BJ}{JD}.\dfrac{1}{2}=1\Rightarrow\dfrac{BJ}{JD}=\dfrac{2}{3}\)
Menelaus cho tam giác CQI:
\(\dfrac{ID}{DC}.\dfrac{CB}{BQ}.\dfrac{QJ}{JI}=1\Rightarrow1.4.\dfrac{JQ}{JI}=1\Rightarrow\dfrac{JQ}{JI}=\dfrac{1}{4}\)
\(\Rightarrow\dfrac{JB}{JD}+\dfrac{JQ}{JI}=\dfrac{2}{3}+\dfrac{1}{4}=\dfrac{11}{12}\)

Ta có:
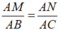
suy ra MN // BC (1) (Định lý Ta-lét đảo).
- Lại có: MN ∩ (MNI) (2)
- Từ (1) và (2) suy ra: BC // (MNI)

Trong mp(BCD), gọi E là giao điểm của JK và CD
Ta có: \(IE\cap AD=\left\{F\right\}\)
\(IE\subset\left(IJK\right)\)
Do đó: \(AD\cap\left(IJK\right)=F\)
Xét ΔACD có I,F,E thẳng hàng
nên \(\dfrac{AI}{IC}\cdot\dfrac{CE}{ED}\cdot\dfrac{DF}{FA}=1\)
=>\(1\cdot2\cdot\dfrac{DF}{FA}=1\)
=>\(\dfrac{FD}{FA}=\dfrac{1}{2}\)
=>\(\dfrac{FA}{FD}=2\)

Đáp án D
![]()
Ta chia khối đa diện thành các khối tứ diện
![]()
Thể tích khối tứ diện đều đã cho là V o = 2 12
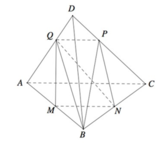
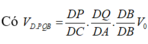
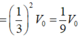
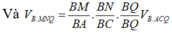
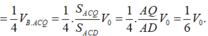
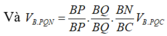
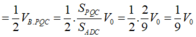
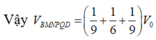
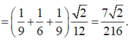

Ta sẽ áp dụng Menelaus cho 2 tam giác BCD và ABC
À quên cái dạo đầu :v
Vì lười chụp hình nên đánh máy vậy
Tìm giao điểm giữa CD và (MNQ) trước
Gán CD vô (BCD) => giao tuyến giữa (BDC) và (MNQ) là QK (K là giao điểm của MN với BC)
=> QK cắt CD tại P => (MNQ) cắt CD tại P
Rồi giờ áp dụng Menelaus cho tam giác ABC trước
\(\dfrac{AM}{MB}.\dfrac{BK}{KC}.\dfrac{CN}{NA}=1\Leftrightarrow\dfrac{1}{2}.\dfrac{BK}{KC}.1=1\Rightarrow BK=2KC\)
Áp dụng Menelaus cho tam giác BCD
\(\dfrac{BK}{KC}.\dfrac{CP}{PD}.\dfrac{DQ}{QB}=1\Leftrightarrow2.\dfrac{CP}{PD}.1=1\Rightarrow CP=\dfrac{1}{2}PD\)
\(\Rightarrow\dfrac{CP}{CD}=\dfrac{1}{3}\)