Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Các đường thẳng MN, NP, PQ, QM cùng nằm trong một mặt phẳng và BC, AD cùng song song với mặt phẳng (MNPQ). Suy ra ba vecto M P → , B C → , A D → đồng phẳng
Đáp án B

Phương án A sai vì : Ba đường thẳng AB, MN, CA cùng trong mặt phẳng (ABC) nên ba vecto A B → , M N → , C A → đồng phẳng
Phương án B sai vì: hai đường thẳng BC, AD cùng song song với mặt phẳng (MNPQ) có chứa đường thẳng MP nên ba vecto M P → , B C → , A D → đồng phẳng
Phương án C sai vì : Đường thẳng AD // (MNPQ) và mặt phẳng này chứa hai đường thẳng MP, PQ nên ba vecto A D → , M P → , P Q → đồng phẳng
Phương án D đúng vì : Đường thẳng BD cắt mặt phẳng (MNPQ) và nó chứa hai đường thẳng MP, PQ nên M P → , P Q → , P D → không đồng phẳng
Đáp án D

Có thể loại các phương án A, B và D vì các cặp ba vecto ( M P → , M B → , v à Q C → ) , ( M P → , M N → , P D → ) và ( M P → , M N → v à Q C → ) đều không đồng phẳng.
Phương án C đúng vì : M P → = M A → + A P → = M A → - m P D →
Đáp án C

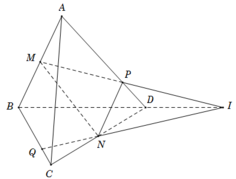
Ta có giao tuyến của 2 mp (ABD) và (BCD) là BD.
Lại có I ∈ M P ⊂ A B D I ∈ N Q ⊂ B C D ⇒ I thuộc giao tuyến của (ABD) và (BCD).
=> I thuộc BD => 3 điểm I; B; D thẳng hàng.
Chọn B.

tham khảo:

Gọi I là trung điểm của BD.
Tam giác BCD có IM là đường trung bình nên IM//DC và IM=\(\dfrac{1}{2}\)CD=\(\dfrac{1}{2}\).2a=1
Tam giác ABD có IN là đường trung bình nên IN//AB và IN=\(\dfrac{1}{2}\)AB=\(\dfrac{1}{2}\).2a=1
Ta có: cos\(\widehat{MIN}\)=\(\dfrac{a^2+a^2-\left(a\sqrt{3}\right)^2}{2.a.a}=\dfrac{-1}{2}\)
Nên \(\widehat{MIN}\)=\(120^0\)
Do AB//IN, CD//IM nên góc giữa AB và CD là góc giữa IM và IN là bằng \(120^0\)
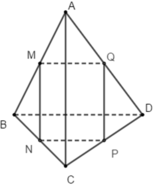

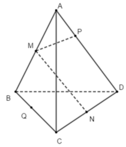
Ta có: M và N lần lượt là trung điểm của AB và BC nên MN là đường trung bình của tam giác ABC
suy ra: MN// AC và M N = 1 2 A C (1)
Tương tự: QP là đường trung bình của tam giác ACD nên QP // AC và Q P = 1 2 A C (2)
Từ (1) và (2) suy ra: tứ giác MNPQ là hình bình hành (có các cạnh đối song song và bằng nhau)
Đáp án C