Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo:
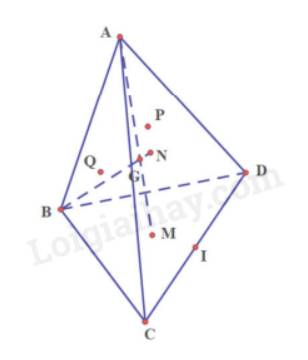
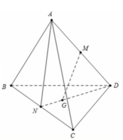
a) Ta có: M là trọng tâm của tam giác BCD
Nên M nằm trên trung tuyến BI (1)
Ta có: N là trọng tâm của tam giác ACD
Nên N nằm trên trung tuyến AI (2)
Từ (1) và (2) suy ra M và N thuộc mp (ABI)
b) Gọi H, K lần lượt là trung điểm của AG, BG
Ta có: HK // AB
AB // MN
Suy ra MN // HK
Theo định lý Ta-let, ta có: \(\frac{{GM}}{{GH}} = \frac{{GN}}{{GK}} = \frac{{MN}}{{HK}}(1)\)
Ta có:\(\frac{{HK}}{{AB}} = \frac{1}{2},\frac{{MN}}{{AB}} = \frac{1}{3}\)
Do đó \(\frac{{MN}}{{AB}}:\frac{{HK}}{{AB}} = \frac{2}{3} \Rightarrow \frac{{MN}}{{HK}} = \frac{2}{3}(2)\)
Từ (1) và (2) suy ra\(\frac{{GM}}{{GH}} = \frac{2}{3}GH = \frac{1}{2}GA \Rightarrow \frac{{GM}}{{\frac{1}{2}GA}} = \frac{2}{3} \Rightarrow \frac{{GM}}{{GA}} = \frac{1}{3}\)
Chứng minh tương tự ta được\(\frac{{GN}}{{GB}} = \frac{1}{3}\)
c) Gọi H, K lần lượt là trung điểm của BC, BD
Tam giác AHD có:\(\frac{{HM}}{{HD}} = \frac{{HQ}}{{HA}} = \frac{1}{3}\)
Suy ra: QM // AD
Do đó, tam giác QGM đồng dạng với tam giác DGA
Nên D, G, Q thẳng hàng
Ta có: QM // AD nên \(\frac{{QM}}{{AD}} = \frac{{HM}}{{HD}} = \frac{{HQ}}{{HA}} = \frac{1}{3}\)
Mà \(\frac{{QM}}{{AD}} = \frac{{QG}}{{GD}}\)
Do đó:\(\frac{{QG}}{{GD}} = \frac{1}{3}\)
Chứng minh tương tự ta được\(\frac{{GP}}{{GC}} = \frac{1}{3}\)
Suy ra điều cần chứng minh.

Đáp án C
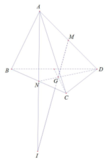
Xét (AND) có MG ∩ AN = I
Mà AN ∈ (ABC)
⇒ MG ∩ (ABC) = I

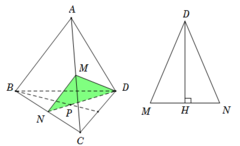
Trong tam giác BCD có: Plà trọng tâm, N là trung điểm BC .
Suy ra N; P; D thẳng hàng.
Vậy thiết diện là tam giác MND..
Xét tam giác MND, ta có M N = A B 2 = a ; D M = D N = A D 3 2 = a 3
Do đó tam giác MND cân tại D.
Gọi H là trung điểm MN suy ra DH và MN vuông góc với nhau..
Diện tích tam giác S Δ M N D = 1 2 M N . D H = 1 2 M N . D M 2 − M H 2 = a 2 11 4
Chọn C.

1/ \(\overrightarrow{AM}=3\overrightarrow{AM}+\overrightarrow{MB}+\overrightarrow{MC}+\overrightarrow{MD}\)
\(\Leftrightarrow2\overrightarrow{AM}+3\overrightarrow{MG}=\overrightarrow{0}\)
\(\Leftrightarrow2\overrightarrow{AM}+3\overrightarrow{MA}+3\overrightarrow{AG}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{AM}=3\overrightarrow{AG}\)
Ban tu ket luan
2/ Bạn coi lại đề bài, đẳng thức kia có vấn đề. 2k-1IB??
\(\overrightarrow{IA}+2k-1+\overrightarrow{IB}+k\overrightarrow{IC}+\overrightarrow{ID}=0\)
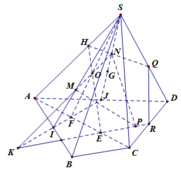



Do I là trọng tâm \(\Rightarrow\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=\overrightarrow{0}\)
\(\Rightarrow\overrightarrow{IA}+\overrightarrow{AB}+\overrightarrow{IA}+\overrightarrow{AC}+\overrightarrow{IA}+\overrightarrow{AD}=\overrightarrow{0}\)
\(\Rightarrow\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}=3\overrightarrow{AI}\) (1)
Đặt \(\overrightarrow{AI}=x.\overrightarrow{AS}\) (2)
Từ giả thiết:
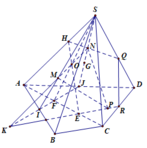
\(AM=2MB\Rightarrow\overrightarrow{AM}=2\overrightarrow{MA}+2\overrightarrow{AB}\Rightarrow\overrightarrow{AM}=\dfrac{2}{3}\overrightarrow{AB}\) \(\Rightarrow\overrightarrow{AB}=\dfrac{3}{2}\overrightarrow{AM}\) (3)
\(\overrightarrow{AN}=\overrightarrow{NC}=\overrightarrow{NA}+\overrightarrow{AC}\Rightarrow\overrightarrow{AN}=\dfrac{1}{2}\overrightarrow{AC}\) \(\Rightarrow\overrightarrow{AC}=2\overrightarrow{AN}\) (4)
\(\overrightarrow{AP}=3\overrightarrow{PD}=3\overrightarrow{PA}+\overrightarrow{AD}\Rightarrow\overrightarrow{AP}=\dfrac{3}{4}\overrightarrow{AD}\) \(\Rightarrow\overrightarrow{AD}=\dfrac{4}{3}\overrightarrow{AP}\) (5)
Thế (2);(3);(4);(5) vào (1):
\(\dfrac{3}{2}\overrightarrow{AM}+2\overrightarrow{AN}+\dfrac{4}{5}\overrightarrow{AP}=3x.\overrightarrow{AS}\)
\(\Rightarrow\overrightarrow{AS}=\dfrac{1}{2x}\overrightarrow{AM}+\dfrac{2}{3x}\overrightarrow{AN}+\dfrac{4}{15x}\overrightarrow{AP}\)
Theo định lý về đồng phẳng, do S, M, N, P đồng thẳng nên:
\(\dfrac{1}{2x}+\dfrac{2}{3x}+\dfrac{4}{15x}=1\) \(\Rightarrow x=\dfrac{43}{30}\)
Ủa có nhầm gì ko mà số xấu ta
Định lý về đồng phẳng đã nói ở đây, phần này rất hay sử dụng trong toán tỉ lệ không gian nên em nhớ là tốt nhất:
Cho hình chóp S.ABCD có đáy là hình bình hành. Lấy điểm M sao cho \(\overrightarrow{MA}+\overrightarrow{MB}+\overrightar... - Hoc24