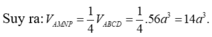Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
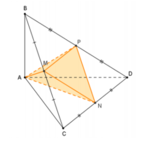
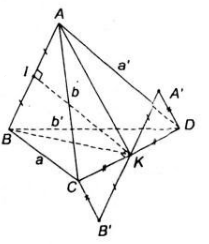
(Vẽ hình: A là đỉnh của tứ diện, BCD là đáy của tứ diện)
+ Trên mặt phẳng đáy BCD kẻ các đường cao của tam giác BCD là BE, CF, DK.Ba đường cao gặp nhau tại H.
+ Xét mặt phẳng ABE
CD vuông góc BE
CD vuông góc AB
=> CD vuông góc với mặt phẳng ABE => CD vuông góc với AH (1)
+ Xét mặt phẳng ACF
BD vuông góc AC
BD vuông góc CF
=> BD vuông góc với mặt phẳng ACF => BD vuông góc với AH (2)
+ Từ (1) và (2) => AH vuông góc BCD
=> AH vuông góc với BC
Mà BC vuông góc với DK
=> BC vuông góc với mp ADK => BC vuông góc với AD
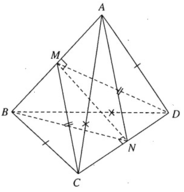
Hai tam giác ABC và BAD bằng nhau ( c.c.c) nên có các đường trung tuyến tương ứng bằng nhau: CM = DM
Ta có tam giác MCD cân tại M, do đó MN ⊥ CD vì N là trung điểm của CD. Tương tự ta chứng minh được NA = NB và suy ra MN ⊥ AB. Mặt phẳng (CDM) không vuông góc với mặt phẳng (ABN) vì (CDM) chứa MN vuông góc với chỉ một đường thẳng AB thuộc (ABN) mà thôi.
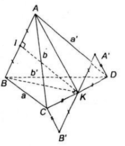
Gọi I, K lần lượt là trung điểm của cạnh AB và CD
Qua K kẻ đường thẳng d // AB, trên d lấy A', B' sao cho K là trung điểm của A'B' và
KA' = IA
* Xét tam giác CKB’ và DKA’ có:
KC= KD ( giả thiết)
KB’= KA’( cách dựng)
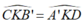( hai góc đối đỉnh )
=> ∆ CKB’ = ∆ DKA’ ( c.g.c)
=> B’C = A’D
*Xét tứ giác IBB’K có IB= KB’ và IB // KB’ ( cách dựng)
=> Tứ giác IBB’K là hình bình hành
=> BB’ // IK (1)
Chứng minh tương tự, ta có: AA’// IK (2)
Từ (1) và (2) suy ra: BB’// IK// AA’ (*)
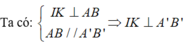
Lại có:IK ⊥ CK
=> IK ⊥ (CKB') (**)
Từ (*) và (**) suy ra BB' ⊥ (CKB') ; AA' ⊥ (CKB')
⇒ BB' ⊥ B'C; AA' ⊥ A'D
* Xét hai tam giác vuông BCB’ và ADA’ có:
BB’ = AA’ (= IK)
CB’ = A’D (chứng minh trên)
=> ∆ BCB’ = ∆ ADA’ ( cạnh huyền –cạnh góc vuông)
=> BC= AD.
* Chứng minh tương tự, AC = BD
AB vuông góc BC
AB vuông góc BD
=>AB vuông góc (BCD)
=>AB vuông góc CD
BC vuông góc CD
AB vuông góc CD
=>CD vuông góc (BCA)
=>CD vuông góc BH
=>(BH;CD)=90 độ
Đáp án D
Áp dụng công thức sau
Với a,b,c là độ dài từng cặp cạnh đối.