Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án A
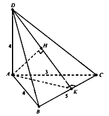
Vì B C 2 = B A 2 + A C 2 nên ∆ A B C vuông tại A.
Gọi K là hình chiếu của A lên BC, H là hình chiếu của A lên DK.
Ta có 1 A H 2 = 1 A D 2 + 1 A K 2 = 1 A D 2 + 1 A B 2 + 1 A C 2
= 1 4 2 + 1 4 2 + 1 3 2 = 17 72 ⇒ d A ; A B C D = A H = 72 17 = 12 34
Đáp án C
Phương pháp giải:
Áp dụng công thức tính nhanh thể tích của tứ diện gần đều, đưa bài toán tính khoảng cách về bài toán tìm thể tích chia cho diện tích đáy (tính theo công thức Hê – rông)
Lời giải:
Đáp án A
Gọi H là hình chiếu của điểm A trên mặt phẳng(BCD). Do ABCD là tứ diện đều nên tâm H là tâm đường trong ngoại tiếp Δ B C D .
Đặt cạnh của tứ diện là a. Gọi M là trung điểm của CD.
Do Δ B C D đều nên
B M = a 3 2 ⇒ B H = 2 3 B M = 2 3 . a 3 2 = a 3 3
Ta có Δ A B H vuông tại H nên
A H = A B 2 − B H 2 = a 2 − a 3 3 2 = a 6 3
Từ giả thiết ta có
A H = a 6 3 = 6 ⇔ a = 3 6 ⇒ S Δ B C D = a 2 3 4 = 27 3 2
(đvdt).
Vậy thể tích của tứ diện ABCD là
A H = a 6 3 = 6 ⇔ a = 3 6 ⇒ S Δ B C D = a 2 3 4 = 27 3 2
(đvtt).
Đáp án B
Gọi O là tâm của tam giác BCD và M là trung điểm CD
⇒
A
O
⊥
(
B
C
D
)
⇒
d
A
;
B
C
D
=
A
O
=
6
Đặt độ dài cạnh của tứ diện ABCD là x ⇒ B O = 2 B M 3 = x 3 3
⇒ A O = A B 2 - B O 2 = x 6 3 = 6 ⇔ x = 3 6
⇒ V = S B C D . A O 3 = x 2 3 . A O 12 = 27 3
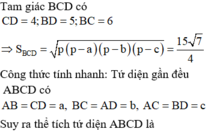
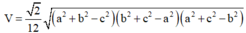
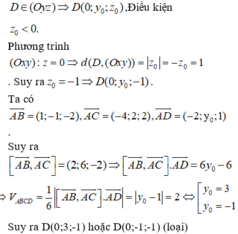
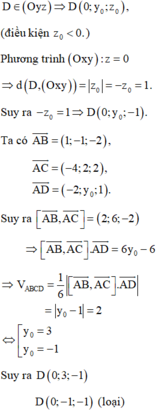
Chọn A
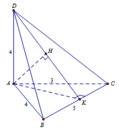
Gọi P là hình chiếu vuông góc của A trên cạnh BC và H là hình chiếu vuông góc của A trên DP.
Khi đó d ( A , ( B C D ) ) = A H = 6 7