K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
KV
1 tháng 9 2023
Do AB // CD (gt)
⇒ ∠ABD = ∠CDB (so le trong)
Xét ∆ABD và ∆CDB có:
AB = CD (gt)
∠ABD = ∠CDB (cmt)
BD chung
⇒ ∆ABD = ∆CDB (c-g-c)
⇒ AD = BC (hai cạnh tương ứng)
Do ∆ABD = ∆CDB (cmt)
⇒ ∠ADB = ∠CBD (hai góc tương ứng)
Mà ∠ADB và ∠CBD là hai góc so le trong
⇒ AD // BC
25 tháng 8 2023
1: Xét tứ giác ABEC có
AB//EC
AC//BE
=>ABEC là hình bình hành
=>BE=AC
mà AC=BD
nên BE=BD
2:
ΔBED cân tại B
mà BH là đường cao
nên H là trung điểm của DE
3: Xét ΔABC và ΔBAD có
BA chung
BC=AD
AC=BD
Do đó: ΔABC=ΔBAD
=>góc OAB=góc OBA
=>OA=OB
OA+OC=AC
OB+OD=BD
mà OA=OB và AC=BD
nên OC=OD
H9
HT.Phong (9A5)
CTVHS
30 tháng 8 2023
a) \(16x^2-1\)
\(=\left(4x\right)^2-1^2\)
\(=\left(4x-1\right)\left(4x+1\right)\)
b) \(\left(x+2\right)^2-49y^2\)
\(=\left(x+2\right)^{^2}-\left(7y\right)^2\)
\(=\left[\left(x+2\right)-7y\right]\left[\left(x+2\right)+7y\right]\)
\(=\left(x+2-7y\right)\left(x+2+7y\right)\)
c) \(4x^2-12xy+9y^2\)
\(=\left(2x\right)^2-2\cdot2x\cdot3y+\left(3y\right)^2\)
\(=\left(2x-3y\right)^2\)
d) \(\left(a+b\right)^2-\left(2a-b\right)^2\)
\(=\left[\left(a+b\right)+\left(2a-b\right)\right]\left[\left(a+b\right)-\left(2a-b\right)\right]\)
\(=\left(a+b+2a-b\right)\left(a+b-2a+b\right)\)
\(=3a\cdot\left(2b-a\right)\)
e) \(\left(x-y\right)^2-2\left(x-y\right)z+z^2\)
\(=\left[\left(x-y\right)-z\right]^2\)
\(=\left(x-y-z\right)^2\)
g) \(-3x^2+6xy-3y^2\)
\(=-\left(3x^2-6xy+3y^2\right)\)
\(=-3\left(x^2-2xy+y^2\right)\)
\(=-3\left(x-y\right)^2\)
30 tháng 8 2023
a: 16x^2-1=(4x)^2-1=(4x-1)(4x+1)
b: (x+2)^2-49y^2
=(x+2)^2-(7y)^2
=(x+2+7y)(x+2-7y)
c: 4x^2-12xy+9y^2=(2x-3y)^2
d: (a+b)^2-(2a-b)^2
=(a+b+2a-b)(a+b-2a+b)
=(2b-a)*3a
g: =-3(x^2-2xy+y^2)
=-3(x-y)^2
T
30 tháng 8 2023
\(a,6a^2b+9ab^2\)
\(=3ab\left(2a+3b\right)\)
\(b,5x^3y^2-15x^2y^3\)
\(=5x^2y^2\left(x-3y\right)\)
\(c,2x\left(x+1\right)-3y\left(x+1\right)\)
\(=\left(x+1\right)\left(2x-3y\right)\)
\(d,\left(x-y\right)^2-x\left(x-y\right)\)
\(=\left(x-y\right)\left(x-y-x\right)\)
\(=-y\left(x-y\right)\)
\(e,y\left(x-1\right)-x\left(1-x\right)\)
\(=y\left(x-1\right)+x\left(x-1\right)\)
\(=\left(x-1\right)\left(y+x\right)\)
\(g,2a\left(a-b\right)+2b\left(b-a\right)\)
\(=2a\left(a-b\right)-2b\left(a-b\right)\)
\(=\left(2a-2b\right)\left(a-b\right)\)
\(=2\left(a-b\right)^2\)
#Urushi☕
30 tháng 8 2023
a: 6a^2b+9ab^2
=3ab*2a+3ab*3b
=3ab(2a+3b)
b: 5x^3y^2-15x^2y^3
=5x^2y^2*x-5x^2y^2*3y
=5x^2y^2(x-3y)
c: 2x(x+1)-3y(x+1)
=(x+1)(2x-3y)
d: =(x-y)(x-y-x)
=-y(x-y)
e: =y(x-1)+x(x-1)
=(x-1)(x+y)
g: =2a(a-b)-2b(a-b)
=(a-b)(2a-2b)
=2(a-b)^2
H9
HT.Phong (9A5)
CTVHS
23 tháng 8 2023
Bài 3:
\(I=64^2-72\cdot64+36^2\)
\(I=64^2-2\cdot36\cdot64+36^2\)
\(I=\left(64-36\right)^2\)
\(I=28^2\)
\(I=784\)
\(K=47\cdot53\)
\(K=\left(50-3\right)\left(50+3\right)\)
\(K=50^2-3^2\)
\(K=2500-9\)
\(K=2491\)
\(M=123^3-69\cdot123^2+369\cdot23^2-23^3\)
\(M=123^3-3\cdot23\cdot123^2+3\cdot123\cdot23^2-23^3\)
\(M=\left(123-23\right)^3\)
\(M=100^3\)
\(M=1000000\)
\(N=54^3+138\cdot54^2+162\cdot46^2+46^3\)
\(N=54^3+3\cdot46\cdot54^2+3\cdot54\cdot46^2+46^3\)
\(N=\left(54+46\right)^3\)
\(N=100^3\)
\(N=1000000\)
KV
23 tháng 8 2023
Bài 1
A = 3(x - 1)² - (x + 1)² + 2(x - 3)(x + 3)
= 3x² - 6x + 1 - x² - 2x - 1 + 2x² - 18
= (3x² - x² + 2x²) + (-6x - 2x) + (1 - 1 - 18)
= 4x² - 8x - 18
B = 5x(x - 7)(x + 7) - 2(2x - 1)²
= 5x³ - 245x - 8x² + 8x - 2
= 5x³ - 8x² + (-245x + 8x) - 2
= 5x³ - 8x² - 237x - 2
C = (x² - 2)(x² + 2) - x² + 4
= x⁴ - 4 - x² + 4
= x⁴ - x²
D = (4x - 1)(1 + 16x + 4x) - (4x + 1)³
= 4x + 80x² - 1 - 20x - 64x³ - 48x² - 12x - 1
= -64x³ + (80x² - 48x²) + (4x - 20x - 12x) + (-1 - 1)
= -64x³ + 32x² - 28x - 2
QA
1
UN
10 tháng 5 2016
Cắt thỏi vàng 7 chỉ ra một khúc một chỉ, một khúc 2 chỉ và khúc còn lại là 4 chỉ. Ngày đầu ông ta đưa người làm một chỉ. Ngày thứ hai đưa 2 chỉ và người làm thối lại ông ta một chỉ. Ngày thứ ba ông ta đưa người làm một chỉ. Ngày thứ tư ông ta đưa người làm 4 chỉ, người đó đưa lại 3 chỉ vàng cho ông nhà giàu. Ngày thứ năm, ông ta đưa một chỉ cho người làm. Ngày thứ sáu ông ta đưa 2 chỉ cho người làm, người làm thối lại một chỉ cho ông ta. Ngày thứ bảy ông ta đưa chỉ vàng còn lại là hết!
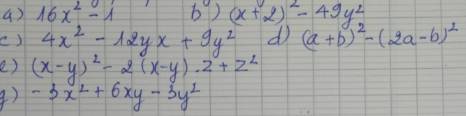
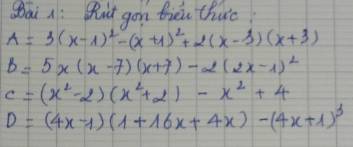
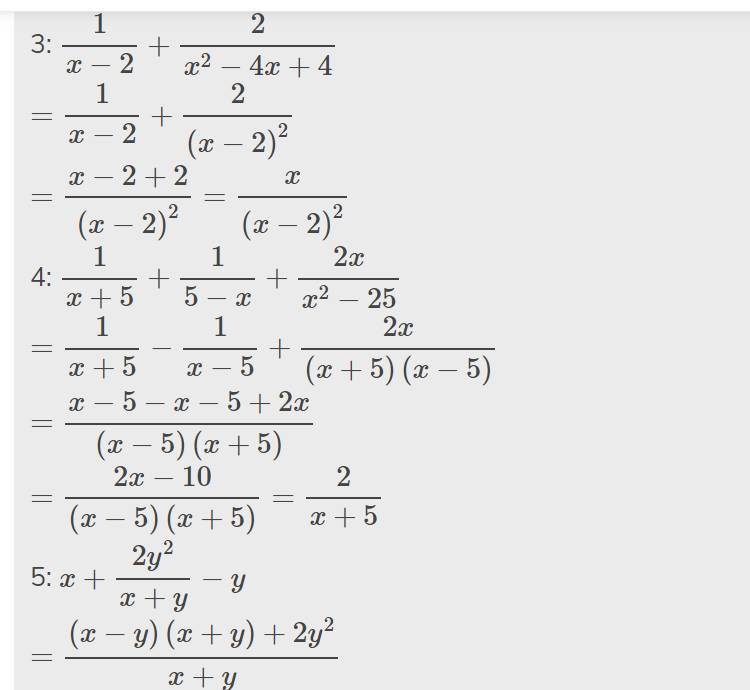
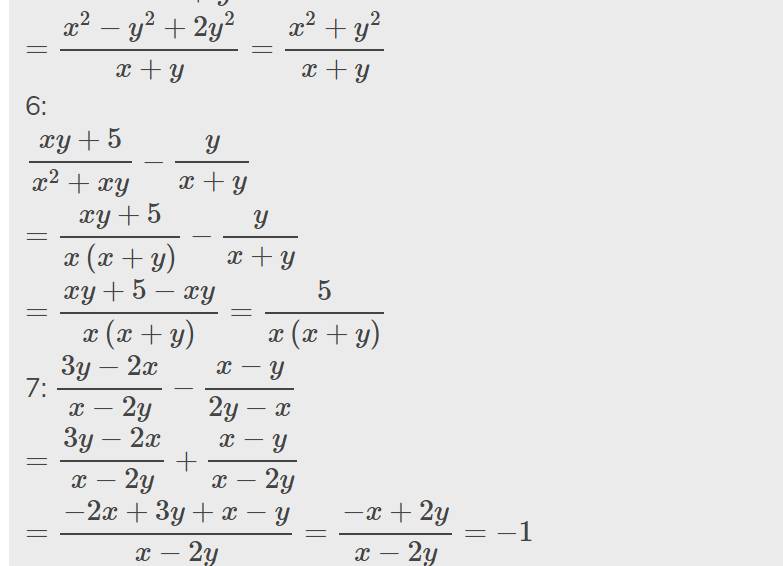
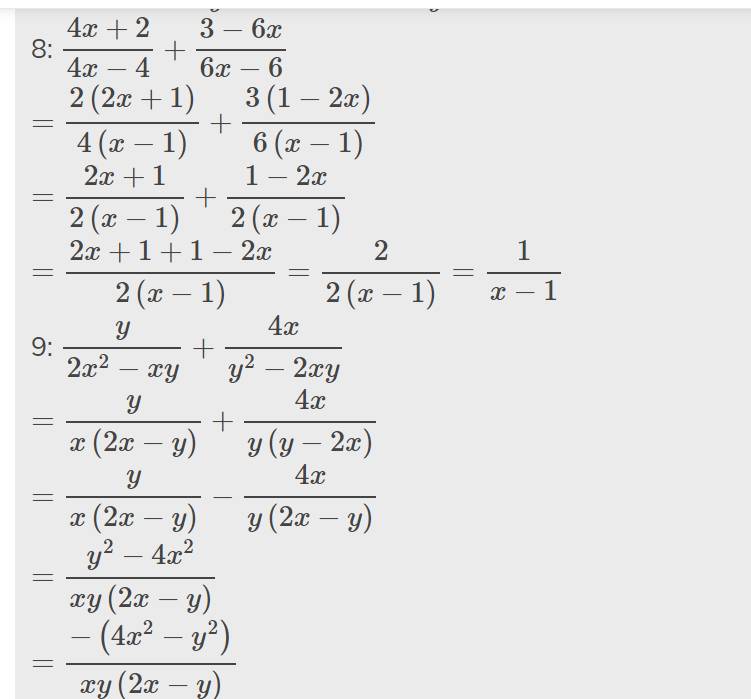
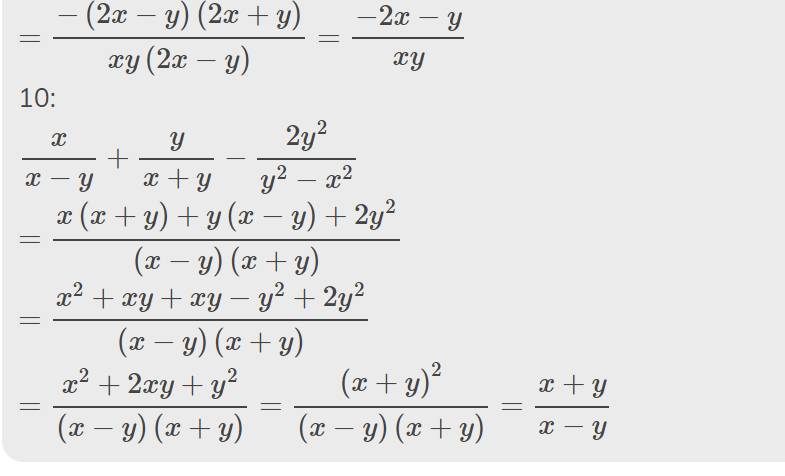
⇒ AD = BC (hai cạnh bên)
∠ADC = ∠BCD (hai góc kề đáy CD)
Xét ∆ADC và ∆BCD có:
AD = BC (cmt)
∠ADC = ∠BCD (cmt)
CD chung
⇒ ∆ADC = ∆BCD (c-g-c)
⇒ ∠ACD = ∠BDC (hai góc tương ứng)
b) Do MN // AB // CD
⇒ ON // AB // CD
Do CD // ON (cmt)
⇒ ∠ACD = ∠NOC (so le trong)
Do CD // AB (gt)
⇒ ∠BDC = ∠ABD (so le trong)
Do AB // ON (cmt)
⇒ ∠ABD = ∠BON (so le trong)
c) Do ∠ACD = ∠NOC (cmt)
∠ACD = ∠BDC (cmt)
⇒ ∠NOC = ∠BDC
Mà ∠BDC = ∠ABD (cmt)
⇒ ∠NOC = ∠ABD
Lại có ∠ABD = ∠BON (cmt)
⇒ ∠NOC = ∠BON
Vậy ON là tia phân giác của ∠BOC