Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

vì BH=9 , HC=16
=> BC=25
xét tam giác ABC ...., ta có
BC^2=CA^2+AB^2
hay 25^2=20^2 +Ab^2
625=400 + AB^2
AB^2=225
AB=15
xét tam giác ABH...., ta có
AB^2=AH^2 + BH^2
hay 15^2= Ah^2 + 9^2
225= AH^2 +81
AH^2= 144
AH=12
thêm kl và những chỗ còn thiếu vào nhé


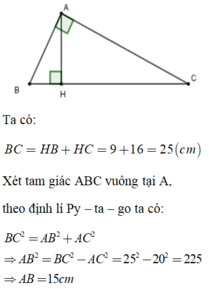
Ta có: \(BC=BH+CH=9+16=25\)
Áp dụng định lý Py- ta - go vào \(\Delta ABC\), ta được:
\(AB^2=BC^2-AC^2\)
\(\Leftrightarrow AB^2=25^2-20^2\)
\(\Leftrightarrow AB^2=625-400\)
\(\Leftrightarrow AB^2=225\)
\(\Leftrightarrow AB=\sqrt{225}=15\)
Áp dụng định lý Py- ta - go vào \(\Delta AHC\), ta được:
\(AH^2=AC^2-CH^2\)
\(\Leftrightarrow AH^2=20^2-16^2\)
\(\Leftrightarrow AH^2=400-256\)
\(\Leftrightarrow AH^2=144\)
\(\Leftrightarrow AH=\sqrt{144}=12\)
Bài làm
BC=BH+HC=9+6=25(cm)BC=BH+HC=9+6=25(cm)
Áp dụng định lý Py-ta-go với tam giác ABC vuông tại A, ta có:
BC2=AB2+AC2BC2=AB2+AC2
⇒AB2=BC2+AC2=252−202⇒AB2=BC2+AC2=252−202
=625−400=225=152=625−400=225=152
Vậy AB=15cm
Áp dụng định lý Py-ta-go với tam giác AHC vuông tại H, ta có:
AH2=AC2−HC2=202−162=122AH2=AC2−HC2=202−162=122
Vậy AH= 12cm
# Học tốt #

a, Ta có : 4AB = 3CA => AB /3 = AC /4 => AB^2/9 = AC^2/16
Theo tính chất dãy tỉ số bằng nhau ta có :
\(\dfrac{AB^2}{9}=\dfrac{AC^2}{16}=\dfrac{BC^2}{25}=\dfrac{400}{25}=16\Rightarrow AB=12cm;AC=16cm\)
b, Ta có : BH + CH = BC = 25 cm
Theo định lí Pytago tam giác ABC vuông tại A
\(AB=\sqrt{BC^2-AC^2}=15cm\)
Theo định lí Pytago tam giác AHB vuông tại H
\(AH=\sqrt{AB^2-HB^2}=12cm\)

ABCH20cm16cm5cm
Áp dụng định lí Pythagoras vào △ABH, ta có :
AB2 = AH2 + BH2
\(\Rightarrow\)202 = AH2 + 162
\(\Rightarrow\)AH2= 144
\(\Rightarrow\)AH = 12
Áp dụng định lí Pythagoras vào △AHC, ta có :
AC2 = AH2 + HC2
\(\Rightarrow\)AC2 = 122 + 52
\(\Rightarrow\)AC2 = 169
\(\Rightarrow\)AC = 13
Vậy AH = 12 cm
AC = 13 cm

Ap dụng định lý Pytago ta có:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow\)\(BC^2=6^2+8^2=100\)
\(\Leftrightarrow\)\(BC=\sqrt{100}=10\)
Ta có hình vẽ: A H B C
Áp dụng định lý Pitago. Ta có:
BC2 = AB2 + AC2 <=> 62 + 82 = 100 cm2
100 = 10 x 10
=> BC = 10 cm
Áp dụng công thức Heron để tính chiều cao. Ta có:
\(S=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}\) (p là chu vi, S là diện tích, a,b,c là độ dài 3 cạnh)
Ta có: Chu vi tam giác là: 6 + 8 + 10 =24 cm
Vậy \(S=\sqrt{24\left(24-6\right)\left(24-8\right)\left(24-10\right)}=48\sqrt{42}\)
Để tính chiều cao AH, ta lấy 2 lần diện tích chia cho đáy ( BC) sẽ có được chiều cao
2 lần diện tích là: \(48\sqrt{42}.2=96\sqrt{42}\)
\(\Rightarrow AH=96\sqrt{42}:10=\frac{24\sqrt{42}}{25}\)
Độ dài cạnh BH là: (Bạn tự làm)
Độ dài cạnh HC là: (Bạn tự làm nhé)

Áp dụng định lý Pi-ta-go vào tam giác vuông ABH vuông tại H ta có:
AB2= BH2 + AH2
<=> 152= 122+ AH2
<=> AH2= 152- 122= 225- 144= 81
<=> AH= 9 (cm)
Tương tự ta có : Áp dụng định lý Pi-ta-go vào tam giác vuông ACH vuông tại H .
AC2= AH2+ HC2
<=> 412= 92+ HC2
<=> HC2= 412- 92= 1681- 81= 1600
<=>HC= 40 (cm)

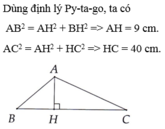
Áp dụng định lí Pytago vào ΔAHC vuông tại H, ta được:
\(AC^2=AH^2+HC^2\)
\(\Leftrightarrow AH^2=AC^2-HC^2=20^2-16^2=144\)
hay AH=12(cm)
Áp dụng định lí Pytago vào ΔAHB vuông tại H, ta được:
\(AB^2=BH^2+AH^2\)
\(\Leftrightarrow AB^2=9^2+12^2=225\)
hay AB=15(cm)
Vậy: AB=15cm; AH=12cm