

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a: Xét ΔQOP có QM/QO=QK/QP
nênMK//OP và MK=OP/2
=>MK//OI và MK=OI
=>OIKM là hình bình hành
mầ góc MOI=90 độ
nên OIKM là hình chữ nhật
b: Để OIKM là hình vuông thì OI=OM
=>OP=OQ
c: \(S_{OPQ}=\dfrac{1}{2}\cdot10\cdot15=75\left(cm^2\right)\)
\(S_{OIKM}=5\cdot7.5=37.5\left(cm^2\right)\)

1: Xét ΔOPQ có
I là trung điểm của PQ
IN//OP
Do đó: N là trung điểm của OQ
Xét ΔOPQ có
I là trung điểm của PQ
IM//OQ
Do đó: M là trung điểm của OP
Xét ΔMPI và ΔNQI có
MP=NQ
\(\widehat{P}=\widehat{Q}\)
PI=QI
Do đó: ΔMPI=ΔNQI
Suy ra: IM=IN
hay ΔIMN cân tại I
2: Ta có: OM=ON
nên O nằm trên đường trung trực của MN(1)
Ta có: IM=IN
nên I nằm trên đường trung trực của MN(2)
Từ (1) và (2) suy ra OI là đường trung trực của MN

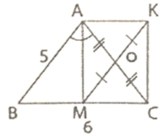
a) Vì M là trung điểm của BC nên:
BM = BC/2 = 6/2 = 3(cm)
Tam giác ABC cân tại A, lại có AM là đường phân giác nên AM cũng là đường cao. Do đó tam giác AMB vuông tại M.
Suy ra: AM2 = AB2 - BM2 (Định lí Pytago)
= 52 - 32 = 16(cm)
Suy ra AM = 4cm
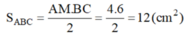
b) ΔAMC vuông tại M có MO là đường trung tuyến nên OM = OA.
Suy ra ∠OAM = ∠OMA ( ΔAMO cân tại O)
Lại có ∠OAM = ∠MAB (AM là tia phân giác góc BAC)
Suy ra ∠OMA = ∠MAB
Mà đây là 2 góc ở vị trí so le trong
Suy ra OM // AB
Vậy tứ giác ABMO là hình thang.
c) Tứ giác AMCK có OA = OC; OM = OK nên tứ giác AMCK là hình bình hành . Lại có ∠AMC = 90o (chứng minh trên) nên tứ giác AMCK là hình chữ nhật.
Hình chữ nhật AMCK là hình vuông
⇔ AM = MC = BM
⇔ AM = BC/2
⇔ ΔABC vuông cân tại A.

Hình bạn tự vẽ chắc dc rùi nhé mình chỉ giải thôi
Bài làm
a/ \(\Delta\)ABC cân tại A có AM là đường trung tuyến ứng với cạnh BC ( M là trung điểm BC )
Nên Am cũng là đường cao \(\Rightarrow\)AM \(⊥\)BC
vì M là trung điểm của BC \(\Rightarrow\)BM= MC = \(\frac{1}{2}BC=\frac{1}{2}.6=3cm\)
Xét tam giác AMB vuông tại M có:
AM2 + BM2 = AB2
AM2 + 32 = 52
AM2 + 9 = 25
AM2 = 25 - 9 =16
\(\Rightarrow\)AM= \(\sqrt{16}=4\)
Vậy S ABC = \(\frac{1}{2}AM.BC\)= \(\frac{1}{2}4.6=12\)
b/ Xét tứ giác AMCN có :
OA=OC (gt)
OM=ON ( N đối xứng với M qua O )
\(\Rightarrow\)Tứ giác AMCN là hình bình hành
Mà AM \(⊥\)MC ( chứng minh ở câu a ) \(\Rightarrow\)\(\widehat{AMC}\)= 90 0
Hình bình hành AMCN có \(\widehat{AMC}=90\)nên AMCN là hình chữ nhật
C/ Để AMNC là hình vuông thì AM phải bằng MC ( Vì theo lý thuyết hcn có 2 cạnh kề bằng nhau là hình vuông )
Nếu tam giác ABC vuông cân tại A thì có :
AM là đường trung tuyến ứng với cạnh huyền BC nên BM = AM = MC
Vậy để tứ giác AMCN là hình vuông thì tam giác ABC phải là tam giác vuông cân tại A

a: Xét tứ giác ANMC có
MN//AC
MN=AC
Do đó: ANMC là hình bình hành

a: MQ=MR=QR/2=12cm
=>PM=5cm
\(S=\dfrac{5\cdot24}{2}=5\cdot12=60\left(cm^2\right)\)
b: Xét tứ giác PMQK có
O là trung điểm chung của PQ và MK
góc PMQ=90 độ
Do đó: PMQK là hình chữ nhật
c: Để PMQK là hình vuông thì PM=MQ=QR/2
=>ΔPQR vuông tại P
=>góc QPR=90 độ